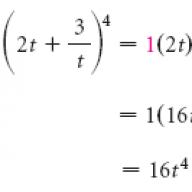Cum se factorizează un număr într-un produs de factori primi. Binomul lui Newton folosind notația factorială

Luați în considerare următoarele expresii cu puteri (a + b) n, unde a + b este orice binom și n este un număr întreg.

Fiecare expresie este un polinom. Puteți observa caracteristici în toate expresiile.

1. În fiecare expresie există un termen în plus decât exponentul n.

2. În fiecare termen suma puterilor este egală cu n, adică. puterea la care este ridicat un binom.

3. Puterile pornesc de la puterea binomiala n si descresc spre 0. Ultimul termen nu are factor a. Primul termen nu are un factor b, adică. grade b încep de la 0 și cresc până la n.

4. Coeficienții încep de la 1 și cresc cu anumite valori până la „jumătate”, apoi scad cu aceleași valori înapoi la 1.

Să aruncăm o privire mai atentă asupra coeficienților. Să presupunem că vrem să aflăm valoarea lui (a + b) 6 . Conform caracteristicii pe care tocmai am observat-o, ar trebui să fie 7 membri aici
a 6 + c 1 a 5 b + c 2 a 4 b 2 + c 3 a 3 b 3 + c 4 a 2 b 4 + c 5 ab 5 + b 6 .
Dar cum putem determina valoarea fiecărui coeficient, c i? Putem face acest lucru în două moduri. Prima metodă implică scrierea coeficienților într-un triunghi, așa cum se arată mai jos. Aceasta este cunoscută ca triunghiul lui Pascal :


Există multe caracteristici în triunghi. Găsiți cât mai multe.
Este posibil să fi găsit o modalitate de a scrie următorul șir de numere folosind numerele de pe linia de mai sus. Unitățile sunt întotdeauna amplasate pe laterale. Fiecare număr rămas este suma celor două numere de deasupra numărului respectiv. Să încercăm să găsim valoarea expresiei (a + b) 6 adăugând următoarea linie, folosind caracteristicile pe care le-am găsit:

Vedem asta în ultima linie

primul și ultimul număr 1 ;
al doilea număr este 1 + 5 sau 6 ;
al treilea număr este 5 + 10 sau 15 ;
al patrulea număr este 10 + 10 sau 20 ;
al cincilea număr este 10 + 5, sau 15 ; Și
al șaselea număr este 5 + 1, sau 6 .

Deci expresia (a + b) 6 va fi egală cu
(a + b) 6 = 1 un 6 + 6 a 5 b + 15 a 4 b 2 + 20 a 3 b 3 + 15 a 2 b 4 + 6 ab 5 + 1 b 6.

Pentru a ridica la puterea (a + b) 8, adăugăm două linii triunghiului lui Pascal:

Apoi
(a + b) 8 = a 8 + 8a 7 b + 28a 6 b 2 + 56a 5 b 3 + 70a 4 b 4 + 56a 3 b 5 + 28a 2 b 6 + 8ab 7 + b 8 .

Putem rezuma rezultatele noastre după cum urmează.

Binomul lui Newton folosind triunghiul lui Pascal

Pentru orice binom a+ b și orice număr natural n,
(a + b) n = c 0 a n b 0 + c 1 a n-1 b 1 + c 2 a n-2 b 2 + .... + c n-1 a 1 b n-1 + c n a 0 b n,
unde numerele c 0 , c 1 , c 2 ,...., c n-1 , c n sunt luate din seria (n + 1) a triunghiului lui Pascal.

Exemplul 1 Ridicare la o putere: (u - v) 5 .

Soluţie Avem (a + b)n, unde a = u, b = -v și n = 5. Folosim al 6-lea rând al triunghiului lui Pascal:
1 5 10 10 5 1
Atunci noi avem
(u - v) 5 = 5 = 1 (u)5+ 5 (u) 4 (-v) 1 + 10 (u) 3 (-v) 2 + 10 (u) 2 (-v) 3 + 5 (u)(-v) 4 + 1 (-v) 5 = u 5 - 5u 4 v + 10u 3 v 2 - 10u 2 v 3 + 5uv 4 - v 5 .
Rețineți că semnele termenilor fluctuează între + și -. Când gradul -v este un număr impar, semnul este -.

Exemplul 2 Ridicare la o putere: (2t + 3/t) 4 .

Soluţie Avem (a + b)n, unde a = 2t, b = 3/t și n = 4. Folosim al 5-lea rând al triunghiului lui Pascal:
1 4 6 4 1
Atunci noi avem

Expansiunea binomială folosind valori factoriale

Să presupunem că vrem să găsim valoarea lui (a + b) 11. Dezavantajul utilizării triunghiului lui Pascal este că trebuie să calculăm toate rândurile anterioare ale triunghiului pentru a obține seria necesară. Următoarea metodă evită acest lucru. De asemenea, vă permite să găsiți un anumit rând - să zicem al 8-lea rând - fără a fi nevoie să evaluați toate celelalte rânduri. Această metodă este utilă în calcule, statistici și utilizări notația coeficientului binomial .
Putem formula binomul lui Newton după cum urmează.

Binomul lui Newton folosind notația factorială

Pentru orice binom (a + b) și orice număr natural n,
.

Binomul lui Newton poate fi demonstrat prin inducție matematică. Arată de ce se numește coeficient binomial .

Exemplul 3 Ridicare la o putere: (x 2 - 2y) 5 .

Soluţie Avem (a + b) n , unde a = x 2 , b = -2y și n = 5. Apoi, folosind binomul lui Newton, avem


În cele din urmă, (x 2 - 2y) 5 = x 10 - 10x 8 y + 40x 6 y 2 - 80x 4 y 3 + 80x 2 y 4 - 35y 5 .

Exemplul 4 Ridicare la o putere: (2/x + 3√x) 4.

Soluţie Avem (a + b)n, unde a = 2/x, b = 3√x și n = 4. Apoi, folosind binomul lui Newton, obținem


În cele din urmă (2/x + 3√x ) 4 = 16/x 4 + 96/x 5/2 + 216/x + 216x 1/2 + 81x 2 .

Găsirea unui anumit membru

Să presupunem că vrem să determinăm unul sau altul termen dintr-o expresie. Metoda pe care am dezvoltat-o ​​ne va permite să găsim acest termen fără a calcula toate rândurile triunghiului lui Pascal sau toți coeficienții anteriori.

Rețineți că în binomul lui Newton ne dă primul termen, ne dă al 2-lea termen, ne dă al 3-lea termen și așa mai departe. Acest lucru poate fi rezumat după cum urmează.

Găsirea termenului (k + 1).

(k + 1) termenul expresiei (a + b) n este .

Exemplul 5 Găsiți al 5-lea termen din expresia (2x - 5y) 6 .

Soluţie Mai întâi, rețineți că 5 = 4 + 1. Atunci k = 4, a = 2x, b = -5y și n = 6. Atunci al 5-lea termen al expresiei va fi

Exemplul 6 Găsiți al 8-lea termen din expresia (3x - 2) 10.

SoluţieÎn primul rând, observăm că 8 = 7 + 1. Atunci k = 7, a = 3x, b = -2 și n = 10. Atunci al 8-lea termen al expresiei va fi

Numărul total de subseturi

Să presupunem că o mulțime are n obiecte. Numărul de submulțimi care conțin k elemente este . Numărul total de submulțimi ale unei mulțimi este numărul de submulțimi cu 0 elemente, precum și numărul de submulțimi cu 1 element, precum și numărul de submulțimi cu 2 elemente și așa mai departe. Numărul total de submulțimi ale unei mulțimi cu n elemente este
.
Acum să ne uităm la ridicarea la puterea (1 + 1) n:

.
Asa de. numărul total de submulțimi este (1 + 1) n, sau 2 n. Am dovedit următoarele.

Numărul total de subseturi

Numărul total de submulțimi ale unei mulțimi cu n elemente este 2n.

Exemplul 7 Câte submulțimi are mulțimea (A, B, C, D, E)?

Soluţie Mulțimea are 5 elemente, apoi numărul de submulțimi este 2 5 sau 32.

Exemplul 8 Lanțul de restaurante Wendy's oferă următoarele toppinguri pentru hamburgeri:
{ketchup, mustar, maioneza, rosii, salata verde, ceapa, ciuperci, masline, branza}.
Câte tipuri diferite de hamburgeri poate oferi Wendy, cu excepția dimensiunilor sau cantităților de hamburgeri?

Soluţie Toppingurile de pe fiecare hamburger sunt membri ai unui subset al setului de toate toppingurile posibile, iar setul gol este doar un hamburger. Numărul total de hamburgeri posibili va fi egal cu

. Astfel, Wendy's poate oferi 512 hamburgeri diferiți.

Orice număr natural poate fi descompus într-un produs de factori primi. Dacă nu vă place să vă ocupați de numere mari precum 5733, aflați cum să le factorați în factori primi (în acest caz, 3 x 3 x 7 x 7 x 13). O problemă similară este adesea întâlnită în criptografie, care se ocupă de problemele de securitate a informațiilor. Dacă nu sunteți încă pregătit să vă creați propriul sistem de e-mail sigur, începeți prin a învăța cum să factorizați numerele în factori primi.

Pași

Partea 1

Găsirea factorilor primi

  1. Începeți cu numărul inițial. Alegeți un număr compus mai mare decât 3. Nu are rost să luați un număr prim, deoarece este divizibil doar cu el însuși și unul.

    • Exemplu: să descompunăm numărul 24 în produsul numerelor prime.

  2. Să descompunăm acest număr în produsul a doi factori. Să găsim două numere mai mici al căror produs este egal cu numărul inițial. Puteți folosi orice factor, dar este mai ușor să folosiți numere prime. O modalitate bună este să încercați să împărțiți numărul inițial mai întâi la 2, apoi la 3, apoi la 5 și să verificați cu care dintre aceste numere prime este divizibil fără a lăsa un rest.

    • Exemplu: Dacă nu cunoașteți factorii pentru numărul 24, încercați să-l împărțiți în numere prime mici. Deci veți descoperi că numărul dat este divizibil cu 2: 24 = 2 x 12. Acesta este un început bun.
    • Deoarece 2 este un număr prim, este bine să îl utilizați atunci când factorați numerele pare.

  3. Începeți să vă construiți arborele multiplicator. Această procedură simplă vă va ajuta să factorați un număr în factorii primi. Pentru a începe, trageți două „ramuri” în jos față de numărul inițial. La sfârșitul fiecărei ramuri scrieți factorii pe care i-ați găsit.

    • Exemplu:

  4. Factorizați următorul șir de numere. Aruncă o privire la cele două numere noi (al doilea rând al arborelui factorilor). Sunt ambele numere prime? Dacă unul dintre ele nu este prim, de asemenea, factorul în doi. Desenați încă două ramuri și scrieți doi factori noi pe a treia linie a copacului.

    • Exemplu: 12 nu este un număr prim, deci trebuie factorizat. Folosim expansiunea 12 = 2 x 6 și o scriem pe a treia linie a arborelui:
    • 2 x 6

  5. Continuați în jos în copac. Dacă unul dintre noii factori se dovedește a fi un număr prim, trageți o „ramură” din el și scrieți același număr la sfârșitul său. Numerele prime nu sunt luate în considerare în numere mai mici, așa că mutați-le la un nivel în jos.

    • Exemplu: 2 este un număr prim. Doar mutați 2 de la a doua la a treia linie:
    • 2 2 6

  6. Continuați factorizarea numerelor până când rămâneți cu numere prime. Verificați fiecare nouă linie a arborelui. Dacă oricare dintre noii factori nu este un număr prim, factorizați-l și scrieți o nouă linie. În cele din urmă, vei rămâne doar cu numere prime.

    • Exemplu: 6 nu este un număr prim, deci trebuie și factorizat. În același timp, 2 este un număr prim și ducem doi doi la următorul nivel:
    • 2 2 6
    • / / /\
    • 2 2 2 3

  7. Scrieți ultima linie ca produs de factori primi.În cele din urmă, vei rămâne doar cu numere prime. Când se întâmplă acest lucru, factorizarea este completă. Ultima linie este un set de numere prime, al căror produs dă numărul inițial.

    • Verificați-vă răspunsul: înmulțiți numerele din ultima linie. Rezultatul ar trebui să fie numărul inițial.
    • Exemplu: Ultimul rând al arborelui factorilor conține numerele 2 și 3. Ambele numere sunt prime, deci factorizarea este completă. Astfel, descompunerea numărului 24 în factori primi este următoarea: 24 = 2 x 2 x 2 x 3.
    • Ordinea factorilor nu contează. Expansiunea poate fi scrisă și ca 2 x 3 x 2 x 2.

  8. Dacă doriți, simplificați răspunsul folosind notația de putere. Dacă sunteți familiarizat cu ridicarea numerelor la puteri, puteți scrie răspunsul într-o formă mai simplă. Amintiți-vă că baza este scrisă în partea de jos, iar numărul suprascriptului arată de câte ori ar trebui să fie înmulțită baza cu ea însăși.

    • Exemplu: de câte ori apare numărul 2 în descompunerea găsită 2 x 2 x 2 x 3? De trei ori, deci expresia 2 x 2 x 2 poate fi scrisă ca 2 3 . În notație simplificată obținem 2 3 x 3.

    Partea 2

    Folosind factorizarea prime

    1. Aflați cel mai mare divizor comun al două numere. Cel mai mare divizor comun (MCD) a două numere este numărul maxim care împarte ambele numere fără a lăsa rest. Exemplul de mai jos arată cum se utilizează descompunerea în factori primi pentru a găsi cel mai mare divisor comun al numerelor 30 și 36.

      • Să factorăm ambele numere în factori primi. Pentru numărul 30, expansiunea este 2 x 3 x 5. Numărul 36 este factorizat după cum urmează: 2 x 2 x 3 x 3.
      • Să găsim un număr care apare în ambele expansiuni. Să tăiem acest număr în ambele liste și să-l scriem pe un rând nou. De exemplu, 2 apare în două expansiuni, așa că scriem 2 pe o linie nouă. Aceasta ne lasă cu 30 = 2 x 3 x 5 și 36 = 2 x 2 x 3 x 3.
      • Repetați această acțiune până când nu mai există factori comuni în expansiuni. Ambele liste conțin și numărul 3, așa că puteți scrie într-un rând nou 2 Și 3 . După aceasta, comparați din nou expansiunile: 30 = 2 x 3 x 5 și 36 = 2 x 2 x 3 x 3. După cum puteți vedea, nu au mai rămas factori comuni în ele.
      • Pentru a găsi cel mai mare factor comun, trebuie să găsiți produsul tuturor factorilor comuni. În exemplul nostru este 2 și 3, deci mcd este 2 x 3 = 6 . Acesta este cel mai mare număr care poate fi împărțit în 30 și 36 fără a lăsa un rest.

    2. Folosind GCD puteți simplifica fracțiile. Dacă bănuiți că o fracție poate fi redusă, utilizați cel mai mare factor comun. Folosind procedura descrisă mai sus, găsiți mcd-ul numărătorului și numitorului. Apoi împărțiți numărătorul și numitorul fracției la acel număr. Ca rezultat, veți obține aceeași fracție într-o formă mai simplă.

      • De exemplu, să simplificăm fracția 30 / 36. După cum am stabilit mai sus, pentru 30 și 36 mcd este 6, așa că împărțim numărătorul și numitorul la 6:
      • 30 ÷ 6 = 5
      • 36 ÷ 6 = 6
      • 30 / 36 = 5 / 6

    3. Să găsim cel mai mic multiplu comun al două numere. Cel mai mic multiplu comun (LCM) a două numere este cel mai mic număr care este divizibil cu ambele numere date fără a lăsa rest. De exemplu, LCM a lui 2 și 3 este 6, deoarece este cel mai mic număr care este divizibil cu 2 și 3. Mai jos este un exemplu de găsire a LCM utilizând factorizarea primelor:

      • Să începem cu două factorizări prime. De exemplu, pentru numărul 126, factorizarea poate fi scrisă ca 2 x 3 x 3 x 7. Numărul 84 este factorizat ca 2 x 2 x 3 x 7.
      • Să comparăm de câte ori apare fiecare factor în expansiuni. Selectați lista în care apare multiplicatorul de numărul maxim de ori și încercuiți-o. De exemplu, numărul 2 apare o dată în listă pentru 126 și de două ori în listă pentru 84, așa că ar trebui să încercuiți 2 x 2în a doua listă de multiplicatori.
      • Repetați acest pas pentru fiecare multiplicator. De exemplu, 3 apare mai des în prima expansiune, așa că ar trebui să-l încercuiești 3 x 3. Numărul 7 apare o dată în ambele liste, așa că încercuiește 7 (nu contează în ce listă, dacă un anumit multiplicator apare în ambele liste de același număr de ori).
      • Pentru a găsi LCM, înmulțiți toate numerele încercuite. În exemplul nostru, cel mai mic multiplu comun al lui 126 și 84 este 2 x 2 x 3 x 3 x 7 = 252. Acesta este cel mai mic număr care este divizibil cu 126 și 84 fără rest.

    4. Utilizați LCM pentru a adăuga fracții. Când adăugați două fracții, trebuie să le aduceți la un numitor comun. Pentru a face acest lucru, găsiți LCM a doi numitori. Apoi înmulțiți numărătorul și numitorul fiecărei fracții cu un astfel de număr încât numitorii fracțiilor să devină egali cu LCM. După aceasta puteți adăuga fracțiile.

      • De exemplu, trebuie să găsiți suma 1/6 + 4/21.
      • Folosind metoda de mai sus, puteți găsi LCM pentru 6 și 21. Este egal cu 42.
      • Să transformăm fracția 1/6 astfel încât numitorul ei să fie egal cu 42. Pentru a face acest lucru, trebuie să împărțiți 42 la 6: 42 ÷ 6 = 7. Acum înmulțiți numărătorul și numitorul fracției cu 7: 1/6 x 7/7 = 7/42.
      • Pentru a aduce a doua fracție la numitorul 42, împărțiți 42 la 21: 42 ÷ 21 = 2. Înmulțiți numărătorul și numitorul fracției cu 2: 4 / 21 x 2 / 2 = 8 / 42.
      • Odată ce fracțiile sunt reduse la același numitor, se pot adăuga cu ușurință: 7/42 + 8/42 = 15/42.

În acest articol veți găsi toate informațiile necesare pentru a răspunde la întrebare, cum se factorizează un număr în factori primi. În primul rând, se oferă o idee generală despre descompunerea unui număr în factori primi și sunt date exemple de descompunere. Următoarele arată forma canonică de descompunere a unui număr în factori primi. După aceasta, este dat un algoritm pentru descompunerea numerelor arbitrare în factori primi și sunt date exemple de descompunere a numerelor folosind acest algoritm. De asemenea, sunt luate în considerare metode alternative care vă permit să factorați rapid numere întregi mici în factori primi folosind teste de divizibilitate și tabele de înmulțire.

Navigare în pagină.

Ce înseamnă factorizarea unui număr în factori primi?

În primul rând, să vedem care sunt factorii primi.

Este clar că, deoarece cuvântul „factori” este prezent în această expresie, atunci există un produs al unor numere, iar cuvântul calificativ „simplu” înseamnă că fiecare factor este un număr prim. De exemplu, într-un produs de forma 2·7·7·23 există patru factori primi: 2, 7, 7 și 23.

Ce înseamnă factorizarea unui număr în factori primi?

Aceasta înseamnă că acest număr trebuie reprezentat ca un produs al factorilor primi, iar valoarea acestui produs trebuie să fie egală cu numărul inițial. Ca exemplu, luați în considerare produsul a trei numere prime 2, 3 și 5, acesta este egal cu 30, deci descompunerea numărului 30 în factori primi este 2·3·5. De obicei, descompunerea unui număr în factori primi se scrie ca o egalitate în exemplul nostru va fi astfel: 30=2·3·5. Subliniem separat faptul că factorii primi ai expansiunii pot fi repetați. Acest lucru este ilustrat clar de următorul exemplu: 144=2·2·2·2·3·3. Dar o reprezentare de forma 45=3·15 nu este o descompunere în factori primi, deoarece numărul 15 este un număr compus.

Apare următoarea întrebare: „Ce numere pot fi descompuse în factori primi?”

În căutarea unui răspuns la acesta, prezentăm următorul raționament. Numerele prime, prin definiție, sunt printre cele mai mari decât unu. Având în vedere acest fapt și , se poate argumenta că produsul mai multor factori primi este un întreg pozitiv mai mare decât unu. Prin urmare, factorizarea are loc numai pentru numerele întregi pozitive care sunt mai mari decât 1.

Dar toate numerele întregi mai mari decât unu pot fi factorizate în factori primi?

Este clar că nu este posibilă factorizarea numerelor întregi simple în factori primi. Acest lucru se datorează faptului că numerele prime au doar doi factori pozitivi - unul și el însuși, deci nu pot fi reprezentate ca produsul a două sau mai multe numere prime. Dacă întregul z ar putea fi reprezentat ca produsul numerelor prime a și b, atunci conceptul de divizibilitate ne-ar permite să concluzionăm că z este divizibil atât cu a cât și cu b, ceea ce este imposibil din cauza simplității numărului z. Cu toate acestea, ei cred că orice număr prim este în sine o descompunere.

Dar numerele compuse? Sunt numerele compuse descompuse în factori primi și toate numerele compuse sunt supuse unei astfel de descompunere? Teorema fundamentală a aritmeticii oferă un răspuns afirmativ la câteva dintre aceste întrebări. Teorema de bază a aritmeticii afirmă că orice număr întreg a care este mai mare decât 1 poate fi descompus în produsul factorilor primi p 1, p 2, ..., p n, iar descompunerea are forma a = p 1 · p 2 · … · p n, iar aceasta expansiunea este unică, dacă nu țineți cont de ordinea factorilor

Descompunerea canonică a unui număr în factori primi

În expansiunea unui număr, factorii primi se pot repeta. Repetarea factorilor primi poate fi scris mai compact folosind . Fie ca în descompunerea unui număr factorul prim p 1 să apară de 1 ori, factorul prim p 2 – s de 2 ori și așa mai departe, p n – s de n ori. Atunci descompunerea în factori primi a numărului a poate fi scrisă ca a=p 1 s 1 ·p 2 s 2 ·…·p n s n. Această formă de înregistrare este așa-numita factorizarea canonică a unui număr în factori primi.

Să dăm un exemplu de descompunere canonică a unui număr în factori primi. Anunță-ne despre descompunere 609 840=2 2 2 2 3 3 5 7 11 11, notația sa canonică are forma 609 840=2 4 3 2 5 7 11 2.

Descompunerea canonică a unui număr în factori primi vă permite să găsiți toți divizorii numărului și numărul de divizori ai numărului.

Algoritm pentru factorizarea unui număr în factori primi

Pentru a face față cu succes sarcinii de a descompune un număr în factori primi, trebuie să aveți o cunoaștere foarte bună a informațiilor din articolul numere prime și compuse.

Esența procesului de descompunere a unui număr întreg pozitiv a care depășește unul este clară din demonstrarea teoremei fundamentale a aritmeticii. Ideea este să găsim secvenţial cei mai mici divizori primi p 1, p 2, ..., p n ai numerelor a, a 1, a 2, ..., a n-1, ceea ce ne permite să obţinem o serie de egalităţi. a=p 1 ·a 1, unde a 1 = a:p 1 , a=p 1 ·a 1 =p 1 ·p 2 ·a 2 , unde a 2 =a 1:p 2 , …, a=p 1 ·p 2 ·…·p n ·a n , unde a n =a n-1:p n . Când obținem a n =1, atunci egalitatea a=p 1 ·p 2 ·…·p n ne va oferi descompunerea dorită a numărului a în factori primi. De asemenea, trebuie remarcat aici că p 1 ≤p 2 ≤p 3 ≤…≤p n.

Rămâne să ne dăm seama cum să găsim cei mai mici factori primi la fiecare pas și vom avea un algoritm pentru descompunerea unui număr în factori primi. Un tabel cu numere prime ne va ajuta să găsim factorii primi. Să arătăm cum să-l folosim pentru a obține cel mai mic divizor prim al numărului z.

Luăm succesiv numere prime din tabelul numerelor prime (2, 3, 5, 7, 11 și așa mai departe) și împărțim numărul dat z la ele. Primul număr prim cu care z este împărțit egal va fi cel mai mic divizor prim al său. Dacă numărul z este prim, atunci cel mai mic divizor prim al său va fi numărul z însuși. Trebuie amintit aici că, dacă z nu este un număr prim, atunci cel mai mic divizor prim al său nu depășește numărul , unde este de la z. Astfel, dacă printre numerele prime care nu depășesc , nu a existat un singur divizor al numărului z, atunci putem concluziona că z este un număr prim (mai multe despre acest lucru sunt scrise în secțiunea teorie de la rubrica Acest număr este prim sau compus ).

Ca exemplu, vom arăta cum să găsiți cel mai mic divizor prim al numărului 87. Să luăm numărul 2. Împărțiți 87 la 2, obținem 87:2=43 (răman de 1) (dacă este necesar, vezi articolul). Adică, când împărțim 87 la 2, restul este 1, deci 2 nu este un divizor al numărului 87. Luăm următorul număr prim din tabelul numerelor prime, acesta este numărul 3. Împărțind 87 la 3, obținem 87:3=29. Astfel, 87 este divizibil cu 3, prin urmare, numărul 3 este cel mai mic divizor prim al numărului 87.

Rețineți că, în cazul general, pentru a factoriza un număr a în factori primi, avem nevoie de un tabel de numere prime până la un număr nu mai mic de . Va trebui să ne referim la acest tabel la fiecare pas, așa că trebuie să-l avem la îndemână. De exemplu, pentru a factoriza numărul 95 în factori primi, vom avea nevoie doar de un tabel cu numere prime până la 10 (deoarece 10 este mai mare decât ). Și pentru a descompune numărul 846.653, veți avea deja nevoie de un tabel cu numere prime până la 1.000 (deoarece 1.000 este mai mare decât ).

Acum avem suficiente informații de notat algoritm pentru factorizarea unui număr în factori primi. Algoritmul de descompunere a numărului a este următorul:

  • Sortând secvențial numerele din tabelul numerelor prime, găsim cel mai mic divizor prim p 1 al numărului a, după care calculăm a 1 =a:p 1. Dacă a 1 =1, atunci numărul a este prim și el însuși este descompunerea lui în factori primi. Dacă a 1 nu este egal cu 1, atunci avem a=p 1 ·a 1 și trecem la pasul următor.
  • Găsim cel mai mic divizor prim p 2 al numărului a 1 , pentru a face acest lucru sortăm succesiv numerele din tabelul numerelor prime, începând cu p 1 , apoi calculăm a 2 =a 1:p 2 . Dacă a 2 =1, atunci descompunerea necesară a numărului a în factori primi are forma a=p 1 ·p 2. Dacă a 2 nu este egal cu 1, atunci avem a=p 1 ·p 2 ·a 2 și trecem la pasul următor.
  • Parcurgând numerele din tabelul numerelor prime, începând cu p 2, găsim cel mai mic divizor prim p 3 al numărului a 2, după care se calculează a 3 =a 2:p 3. Dacă a 3 =1, atunci descompunerea necesară a numărului a în factori primi are forma a=p 1 ·p 2 ·p 3. Dacă a 3 nu este egal cu 1, atunci avem a=p 1 ·p 2 ·p 3 ·a 3 și trecem la pasul următor.
  • Găsim cel mai mic divizor prim p n al numărului a n-1 prin sortarea numerelor prime, începând cu p n-1, precum și a n =a n-1:p n, iar a n este egal cu 1. Acest pas este ultimul pas al algoritmului aici obținem descompunerea dorită a numărului a în factori primi: a=p 1 ·p 2 ·…·p n.

Pentru claritate, toate rezultatele obținute la fiecare pas al algoritmului de descompunere a unui număr în factori primi sunt prezentate sub forma următorului tabel, în care numerele a, a 1, a 2, ..., a n sunt scrise succesiv. într-o coloană la stânga liniei verticale și la dreapta dreptei - cei mai mici divizori primi corespunzători p 1, p 2, ..., p n.

Tot ce rămâne este să luăm în considerare câteva exemple de aplicare a algoritmului rezultat pentru descompunerea numerelor în factori primi.

Exemple de descompunere în factori primi

Acum ne vom uita în detaliu exemple de factorizare a numerelor în factori primi. La descompunere, vom folosi algoritmul din paragraful anterior. Să începem cu cazuri simple și să le complicăm treptat pentru a întâlni toate nuanțele posibile care apar la descompunerea numerelor în factori primi.

Exemplu.

Factorizați numărul 78 în factorii săi primi.

Soluţie.

Începem căutarea primului divizor prim cel mai mic p 1 al numărului a=78. Pentru a face acest lucru, începem să sortăm succesiv numerele prime din tabelul numerelor prime. Luăm numărul 2 și împărțim 78 la el, obținem 78:2=39. Numărul 78 este împărțit la 2 fără rest, deci p 1 =2 este primul divizor prim găsit al numărului 78. În acest caz, a 1 =a:p 1 =78:2=39. Ajungem deci la egalitatea a=p 1 ·a 1 având forma 78=2·39. Evident, un 1 =39 este diferit de 1, așa că trecem la pasul al doilea al algoritmului.

Acum căutăm cel mai mic divizor prim p 2 al numărului a 1 =39. Începem enumerarea numerelor din tabelul numerelor prime, începând cu p 1 =2. Împărțiți 39 la 2, obținem 39:2=19 (răman de 1). Deoarece 39 nu este divizibil egal cu 2, atunci 2 nu este divizor. Apoi luăm următorul număr din tabelul numerelor prime (numărul 3) și împărțim 39 la el, obținem 39:3=13. Prin urmare, p 2 =3 este cel mai mic divizor prim al numărului 39, în timp ce a 2 =a 1:p 2 =39:3=13. Avem egalitatea a=p 1 ·p 2 ·a 2 sub forma 78=2·3·13. Deoarece un 2 =13 este diferit de 1, trecem la pasul următor al algoritmului.

Aici trebuie să găsim cel mai mic divizor prim al numărului a 2 =13. În căutarea celui mai mic divizor prim p 3 al numărului 13, vom sorta succesiv numerele din tabelul numerelor prime, începând cu p 2 =3. Numărul 13 nu este divizibil cu 3, deoarece 13:3=4 (rest. 1), de asemenea 13 nu este divizibil cu 5, 7 și 11, deoarece 13:5=2 (rest. 3), 13:7=1 (rest. 6) și 13:11=1 (rest. 2). Următorul număr prim este 13, iar 13 este divizibil cu el fără rest, prin urmare, cel mai mic divizor prim p 3 din 13 este numărul 13 însuși, iar a 3 =a 2:p 3 =13:13=1. Deoarece a 3 =1, acest pas al algoritmului este ultimul, iar descompunerea dorită a numărului 78 în factori primi are forma 78=2·3·13 (a=p 1 ·p 2 ·p 3 ).

Răspuns:

78=2·3·13.

Exemplu.

Exprimă numărul 83.006 ca produs al factorilor primi.

Soluţie.

La prima etapă a algoritmului de descompunere a unui număr în factori primi, găsim p 1 =2 și a 1 =a:p 1 =83.006:2=41.503, din care 83.006=2·41.503.

În a doua etapă, aflăm că 2, 3 și 5 nu sunt divizori primi ai numărului a 1 =41.503, dar numărul 7 este, deoarece 41.503:7=5.929. Avem p 2 =7, a 2 =a 1:p 2 =41.503:7=5.929. Astfel, 83.006=2 7 5 929.

Cel mai mic divizor prim al numărului a 2 =5 929 este numărul 7, deoarece 5 929:7 = 847. Astfel, p 3 =7, a 3 =a 2:p 3 =5 929:7 = 847, din care 83 006 = 2·7·7·847.

În continuare aflăm că cel mai mic divizor prim p 4 al numărului a 3 =847 este egal cu 7. Atunci a 4 =a 3:p 4 =847:7=121, deci 83 006=2·7·7·7·121.

Acum găsim cel mai mic divizor prim al numărului a 4 =121, acesta este numărul p 5 =11 (deoarece 121 este divizibil cu 11 și nu este divizibil cu 7). Apoi a 5 =a 4:p 5 =121:11=11 și 83 006=2·7·7·7·11·11.

În cele din urmă, cel mai mic divizor prim al numărului a 5 =11 este numărul p 6 =11. Apoi a 6 =a 5:p 6 =11:11=1. Deoarece a 6 =1, acest pas al algoritmului de descompunere a unui număr în factori primi este ultimul, iar descompunerea dorită are forma 83 006 = 2·7·7·7·11·11.

Rezultatul obținut poate fi scris ca descompunerea canonică a numărului în factori primi 83 006 = 2·7 3 ·11 2.

Răspuns:

83 006=2 7 7 7 11 11=2 7 3 11 2 991 este un număr prim. Într-adevăr, nu are un singur divizor prim care să nu depășească ( poate fi estimat aproximativ ca , deoarece este evident că 991<40 2 ), то есть, наименьшим делителем числа 991 является оно само. Тогда p 3 =991 и a 3 =a 2:p 3 =991:991=1 . Следовательно, искомое разложение числа 897 924 289 на простые множители имеет вид 897 924 289=937·967·991 .

Răspuns:

897 924 289 = 937 967 991 .

Utilizarea testelor de divizibilitate pentru factorizarea prime

În cazuri simple, puteți descompune un număr în factori primi fără a utiliza algoritmul de descompunere din primul paragraf al acestui articol. Dacă numerele nu sunt mari, atunci pentru a le descompune în factori primi este adesea suficient să cunoaștem semnele divizibilității. Să dăm exemple pentru clarificare.

De exemplu, trebuie să factorăm numărul 10 în factori primi. Din tabla înmulțirii știm că 2·5=10, iar numerele 2 și 5 sunt evident prime, deci descompunerea în factori primi a numărului 10 arată ca 10=2·5.

Alt exemplu. Folosind tabla înmulțirii, vom factoriza numărul 48 în factori primi. Știm că șase este opt - patruzeci și opt, adică 48 = 6·8. Cu toate acestea, nici 6, nici 8 nu sunt numere prime. Dar știm că de două ori trei este șase și de două ori patru este opt, adică 6=2·3 și 8=2·4. Atunci 48=6·8=2·3·2·4. Rămâne să ne amintim că de două ori doi este patru, atunci obținem descompunerea dorită în factori primi 48 = 2·3·2·2·2. Să scriem această expansiune în formă canonică: 48=2 4 ·3.

Dar atunci când factorizați numărul 3.400 în factori primi, puteți utiliza criteriile de divizibilitate. Semnele divizibilității cu 10, 100 ne permit să afirmăm că 3.400 este divizibil cu 100, cu 3.400=34·100, iar 100 este divizibil cu 10, cu 100=10·10, deci, 3.400=34·10·10. Și pe baza testului de divizibilitate cu 2, putem spune că fiecare dintre factorii 34, 10 și 10 este divizibil cu 2, obținem 3 400=34 10 10=2 17 2 5 2 5. Toți factorii din expansiunea rezultată sunt simpli, așa că această expansiune este cea dorită. Rămâne doar să rearanjați factorii astfel încât să meargă în ordine crescătoare: 3 400 = 2·2·2·5·5·17. Să notăm și descompunerea canonică a acestui număr în factori primi: 3 400 = 2 3 ·5 2 ·17.

Când descompuneți un număr dat în factori primi, puteți utiliza pe rând atât semnele divizibilității, cât și tabla înmulțirii. Să ne imaginăm numărul 75 ca un produs al factorilor primi. Testul divizibilității cu 5 ne permite să afirmăm că 75 este divizibil cu 5 și obținem că 75 = 5·15. Și din tabla înmulțirii știm că 15=3·5, deci, 75=5·3·5. Aceasta este descompunerea necesară a numărului 75 în factori primi.

Bibliografie.

  • Vilenkin N.Ya. si altii. Clasa a VI-a: manual pentru instituţiile de învăţământ general.
  • Vinogradov I.M. Fundamentele teoriei numerelor.
  • Mihailovici Sh.H. Teoria numerelor.
  • Kulikov L.Ya. și altele. Culegere de probleme de algebră și teoria numerelor: Manual pentru studenții de fizică și matematică. specialităţile institutelor pedagogice.

Un caz special al seriei Taylor pentru x 0 =0

nhai sa ne numimaproape Maclaurin pentru functief(X).

Să găsim descompunerea unora elementar funcții din seria Maclaurin.

Exemplul 23


.

Soluţie.

Pentru a rezolva problema vom folosi algoritmul formulat mai sus. Deoarece este necesară extinderea funcției într-o serie Maclaurin, prin urmare, vom căuta o expansiune în vecinătatea punctului X 0 = 0.

Să găsim valoarea funcției în punct X 0 =0, funcții derivate până la P-a ordine și valorile acestora la X 0 = 0:

Să scriem formal seria Maclaurin folosind formula

Rețineți că am obținut rad pentru puteri impare, deoarece coeficienții pentru puteri pare (când P- număr par) sunt egale cu zero.

Să găsim regiunea de convergență a seriei rezultate pentru aceasta compilam o serie de valori absolute ale termenilor seriei:

și aplică-i semnul D'Alembert.

Deoarece valoarea limitei nu depinde de Xși mai puțin de unul pentru oricare X, atunci seria converge pentru toate valorile, ceea ce înseamnă că domeniul de convergență al seriei este X(–,+).

Să verificăm dacă sunt îndeplinite condiții suficiente. Este evident că

Pentru P= 0,1,2,... și pentru orice X,

Aceasta înseamnă că funcția este extinsă în seria sa Maclaurin pe întreaga axă numerică, adică.

la X(–,+).

În exemplul considerat, pentru a determina coeficienții de expansiune a unei funcții într-o serie de puteri în vecinătatea unui punct X 0 =0 am diferențiat succesiv funcția până când am putut deriva o formulă pentru P-a derivată și a găsit valorile derivatelor la un punct dat. Apoi au aflat pentru care X sunt îndeplinite condiţii suficiente pentru descompunebilitatea unei funcţii dintr-o serie. Adesea, acești pași duc la calcule greoaie. Aceste dificultăți pot fi uneori ocolite prin utilizarea afirmație acea Expansiunea unei funcții într-o serie de puteri obținută prin orice metodă va fi extinderea acesteia într-o serie Taylor. Prin urmare, pentru a obține o extindere a unei funcții într-o serie de puteri, se pot folosi expansiunile deja cunoscute ale funcțiilor elementare, seria Maclaurin, aplicând acestora regulile de adunare, înmulțire a seriilor și teoreme privind integrarea și diferențierea serie de puteri.

De exemplu, extinderea funcției f(X)= cos X se poate obţine prin diferenţierea termen cu termen a extinderii seriei Maclaurin a funcţiei f(X) = păcat X.

la X(–,+).

În mod similar, folosind algoritmul de expansiune și teoremele privind integrarea și diferențierea serii de puteri, se pot obține expansiuni în serie Maclaurin ale următoarelor funcții elementare:

la X(–,+);

edacă t≥.0, sau t-1, atunci regiunea de convergență x (-1;1),

edacă–1< T<0 , atunci regiunea de convergență x (-1;1].

Această descompunere se numește serie binomială.În special, presupunând în ultima expansiune T= –1, primim

, X (-1;1).

Înlocuirea în această expansiune X la expresia (– X), primim

, la X (–1;1).

Folosirea teoremei privind integrarea serii de puteri și aplicarea acesteia la extinderea funcției în serie Maclaurin
, primim

la X (–1;1].

Înlocuirea funcțiilor în expansiune
variabil X la expresie și integrăm, obținem

La X [–1;1].

Folosind serie binomială – Extinderea în serie Maclaurin a funcției
, presupunând
, înlocuind X la expresie
și integrând, obținem

La X (–1;1).

Exemplul 24.

Folosind expansiuni cunoscute, extindeți funcția într-o serie Maclaurin
.

Soluţie

Este necesar să se găsească extinderea funcției în seria Maclaurin, i.e. într-o serie de puteri în puteri X. Vom folosi expansiunea

la t  (–1;1].

crezând t = X 2 , primim

Această extindere este valabilă când
, Unde
, apoi regiunea de convergență
.

Prin urmare,

Înmulțirea ambelor părți ale egalității cu X, primim

la X [–1;1].

Pexemplul 25

Folosind expansiuni cunoscute, extindeți funcția
într-o serie Taylor în vecinătatea unui punct X 0 =1.

Soluţie.

Este necesar să se obțină o extindere a funcției într-o serie Taylor în vecinătatea punctului X 0 = 1, acestea. pe grade ( X–1).

Vom folosi expansiunea

La t  (-1;1).

Pentru a obține o extindere a acestei funcții în puteri ( X–1) să introducem o nouă variabilă t= X–1, Apoi x =t + 1. Să transformăm această funcție într-o nouă variabilă, presupunând x =t + 1:

Presupunând în schimb într-o expansiune cunoscută t exprimarea și înmulțirea cu un număr, obținem

la  (-1;1).

Presupunând în expansiunea rezultată t = X–1, să revenim la variabila inițială Xși obținem extinderea acestei funcții într-o serie de puteri în puteri ( X-1):

Această extindere este valabilă în condițiile respective
, Unde
.

Deci, am obținut descompunerea

la
.

Exemplul 26

Extindeți o funcție
într-o serie de puteri la punct
.

Soluţie.

Să transformăm această funcție folosind proprietățile logaritmilor:

Folosind expansiunea cunoscută

la t  (–1;1].

să găsim extinderea funcției
, crezând t= 2X, si functii
, presupunând t= –x:

extinderea este valabilă la 2 X  (–1;1), acestea. la
.

De asemenea,

iar extinderea este valabilă pentru (– X)  (–1;1), adică. la X  (–1;1).

Seriile de putere pot fi adăugate termen cu termen și înmulțite cu un număr, ceea ce înseamnă

Mai mult, această expansiune este valabilă pe regiunea de convergență generală, adică. la
.

Pexemplul 27

Extindeți funcția într-o serie Maclaurin
.

Soluţie.

Să transformăm funcția

.

Folosind binecunoscuta extindere a seriei Maclaurin a funcției la=(1+ t) m , crezând
Și
, primim

Seria binomială utilizată la
are o regiune de convergenţă t  (-1;1], prin urmare, expansiunea rezultată este valabilă pentru
, Unde
,
.

Asa de,
la
.

Dacă funcția f(x) are derivate de toate ordinele pe un anumit interval care conține punctul a, atunci i se poate aplica formula Taylor:
,
Unde r n– așa-numitul termen de rest sau rest al seriei, poate fi estimat folosind formula Lagrange:
, unde numărul x este între x și a.

Reguli de intrare în funcții:

Dacă pentru o anumită valoare X r n→0 la n→∞, atunci în limită formula Taylor devine convergentă pentru această valoare Seria Taylor:
,
Astfel, funcția f(x) poate fi extinsă într-o serie Taylor în punctul x luat în considerare dacă:
1) are derivate de toate ordinele;
2) seria construită converge în acest punct.

Când a = 0 obținem o serie numită lângă Maclaurin:
,
Extinderea celor mai simple funcții (elementare) din seria Maclaurin:
Funcții exponențiale
, R=∞
Funcții trigonometrice
, R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
Funcția actgx nu se extinde în puteri ale lui x, deoarece ctg0=∞
Funcții hiperbolice


Funcții logaritmice
, -1
Seria binomială
.

Exemplul nr. 1. Extindeți funcția într-o serie de puteri f(x)= 2X.
Soluţie. Să găsim valorile funcției și derivatele sale la X=0
f(x) = 2X, f( 0) = 2 0 =1;
f"(x) = 2X ln2, f"( 0) = 2 0 ln2= ln2;
f""(x) = 2X ln 2 2, f""( 0) = 2 0 ln 2 2= ln 2 2;
…
f(n)(x) = 2X ln n 2, f(n)( 0) = 2 0 ln n 2=ln n 2.
Înlocuind valorile obținute ale derivatelor în formula seriei Taylor, obținem:

Raza de convergență a acestei serii este egală cu infinitul, prin urmare această expansiune este valabilă pentru -∞<X<+∞.

Exemplul nr. 2. Scrieți seria Taylor în puteri ( X+4) pentru funcție f(x)= e X.
Soluţie. Aflarea derivatelor functiei e Xși valorile lor la punct X=-4.
f(x)= e X, f(-4) = e -4 ;
f"(x)= e X, f"(-4) = e -4 ;
f""(x)= e X, f""(-4) = e -4 ;
…
f(n)(x)= e X, f(n)( -4) = e -4 .
Prin urmare, seria Taylor necesară a funcției are forma:

Această expansiune este valabilă și pentru -∞<X<+∞.

Exemplul nr. 3. Extindeți o funcție f(x)=ln Xîntr-o serie de puteri ( X- 1),
(adică în seria Taylor în vecinătatea punctului X=1).
Soluţie. Găsiți derivatele acestei funcții.
f(x)=lnx , , , ,

f(1)=ln1=0, f"(1)=1, f""(1)=-1, f"""(1)=1*2,..., f (n) =(- 1) n-1 (n-1)!
Înlocuind aceste valori în formulă, obținem seria Taylor dorită:

Folosind testul lui d'Alembert, puteți verifica dacă seria converge la ½x-1½<1 . Действительно,

Seria converge dacă ½ X- 1½<1, т.е. при 0<X<2. При X=2 se obţine o serie alternativă care satisface condiţiile criteriului Leibniz. Când x=0 funcția nu este definită. Astfel, regiunea de convergență a seriei Taylor este intervalul semideschis (0;2).

Exemplul nr. 4. Extindeți funcția într-o serie de puteri.
Soluţie. În expansiunea (1) înlocuim x cu -x 2, obținem:
, -∞

Exemplul nr. 5. Extindeți funcția într-o serie Maclaurin .
Soluţie. Avem
Folosind formula (4), putem scrie:

înlocuind –x în loc de x în formulă, obținem:

De aici găsim: ln(1+x)-ln(1-x) = -
Deschidem parantezele, rearanjam termenii seriei și aducem termeni similari, obținem
. Această serie converge în intervalul (-1;1), deoarece se obține din două serii, fiecare dintre acestea convergând în acest interval.

cometariu .
Formulele (1)-(5) pot fi, de asemenea, utilizate pentru a extinde funcțiile corespunzătoare într-o serie Taylor, de exemplu. pentru extinderea funcțiilor în puteri întregi pozitive ( Ha). Pentru a face acest lucru, este necesar să se efectueze astfel de transformări identice asupra unei anumite funcții pentru a obține una dintre funcțiile (1)-(5), în care în schimb X costă k( Ha) m , unde k este un număr constant, m este un întreg pozitiv. Este adesea convenabil să faceți o schimbare a variabilei t=Hași extindeți funcția rezultată în raport cu t în seria Maclaurin.

Această metodă se bazează pe teorema privind unicitatea expansiunii unei funcții într-o serie de puteri. Esența acestei teoreme este că în vecinătatea aceluiași punct nu se pot obține două serii de puteri diferite care ar converge către aceeași funcție, indiferent de modul în care este realizată expansiunea acesteia.

Exemplul nr. 5a. Extindeți funcția într-o serie Maclaurin și indicați regiunea de convergență.
Soluţie. Mai întâi găsim 1-x-6x 2 =(1-3x)(1+2x) , .
la elementar:

Fracția 3/(1-3x) poate fi considerată ca fiind suma unei progresii geometrice infinit descrescătoare cu un numitor de 3x, dacă |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

cu regiunea de convergenţă |x|< 1/3.

Exemplul nr. 6. Extindeți funcția într-o serie Taylor în vecinătatea punctului x = 3.
Soluţie. Această problemă poate fi rezolvată, ca și înainte, folosind definiția seriei Taylor, pentru care trebuie să găsim derivatele funcției și valorile acestora la X=3. Cu toate acestea, va fi mai ușor să utilizați extinderea existentă (5):
=
Seria rezultată converge la sau –3

Exemplul nr. 7. Scrieți seria Taylor în puteri (x -1) ale funcției ln(x+2) .
Soluţie.


Seria converge la , sau -2< x < 5.

Exemplul nr. 8. Extindeți funcția f(x)=sin(πx/4) într-o serie Taylor în vecinătatea punctului x =2.
Soluţie. Să facem înlocuirea t=x-2:

Folosind expansiunea (3), în care înlocuim π / 4 t în locul lui x, obținem:

Seria rezultată converge către funcția dată la -∞< π / 4 t<+∞, т.е. при (-∞Prin urmare,
, (-∞

Calcule aproximative folosind seria de puteri

Seriile de putere sunt utilizate pe scară largă în calcule aproximative. Cu ajutorul lor, puteți calcula valorile rădăcinilor, funcțiilor trigonometrice, logaritmilor numerelor și integralelor definite cu o precizie dată. Seriile sunt de asemenea folosite la integrarea ecuațiilor diferențiale.
Luați în considerare expansiunea unei funcții într-o serie de puteri:

Pentru a calcula valoarea aproximativă a unei funcții într-un punct dat X, aparținând regiunii de convergență a seriei indicate, primele sunt lăsate în extinderea acesteia n membri ( n– un număr finit), iar termenii rămași sunt eliminați:

Pentru a estima eroarea valorii aproximative obținute, este necesar să se estimeze restul aruncat rn (x) . Pentru a face acest lucru, utilizați următoarele tehnici:
  • dacă seria rezultată este alternativă, atunci se utilizează următoarea proprietate: pentru o serie alternativă care îndeplinește condițiile Leibniz, restul seriei în valoare absolută nu depășește primul termen aruncat.
  • dacă o serie dată este de semn constant, atunci seria compusă din termeni aruncați este comparată cu o progresie geometrică infinit descrescătoare.
  • în cazul general, pentru a estima restul seriei Taylor, puteți utiliza formula Lagrange: a X ).

Exemplul nr. 1. Calculați ln(3) la cel mai apropiat 0,01.
Soluţie. Să folosim expansiunea unde x=1/2 (vezi exemplul 5 din subiectul anterior):

Să verificăm dacă putem elimina restul după primii trei termeni ai expansiunii pentru a face acest lucru, îl vom evalua folosind suma unei progresii geometrice infinit descrescătoare:

Deci, putem arunca acest rest și obținem

Exemplul nr. 2. Calculați cu cel mai apropiat 0,0001.
Soluţie. Să folosim seria binomială. Deoarece 5 3 este cubul unui număr întreg cel mai apropiat de 130, este recomandabil să se reprezinte numărul 130 ca 130 = 5 3 +5.



deoarece deja cel de-al patrulea termen al seriei alternative rezultate care satisface criteriul Leibniz este mai mic decât precizia cerută:
, astfel încât acesta și termenii care îi urmează pot fi eliminate.
Multe integrale definite sau improprii practic necesare nu pot fi calculate folosind formula Newton-Leibniz, deoarece aplicarea acesteia este asociată cu găsirea unei antiderivate, care adesea nu are expresie în funcții elementare. De asemenea, se întâmplă că găsirea unui antiderivat este posibilă, dar necesită o forță de muncă inutilă. Cu toate acestea, dacă funcția integrand este extinsă într-o serie de puteri, iar limitele integrării aparțin intervalului de convergență al acestei serii, atunci este posibil un calcul aproximativ al integralei cu o precizie predeterminată.

Exemplul nr. 3. Calculați integrala ∫ 0 1 4 sin (x) x până la 10 -5 .
Soluţie. Integrala nedefinită corespunzătoare nu poate fi exprimată în funcții elementare, adică. reprezintă o „integrală nepermanentă”. Formula Newton-Leibniz nu poate fi aplicată aici. Să calculăm integrala aproximativ.
Împărțirea termen cu termen a seriei pentru păcat X pe X, primim:

Integrând această serie termen cu termen (acest lucru este posibil, întrucât limitele de integrare aparțin intervalului de convergență al acestei serii), obținem:

Deoarece seria rezultată satisface condițiile lui Leibniz și este suficient să luăm suma primilor doi termeni pentru a obține valoarea dorită cu o precizie dată.
Astfel, găsim
.

Exemplul nr. 4. Calculați integrala ∫ 0 1 4 e x 2 cu o precizie de 0,001.
Soluţie.
. Să verificăm dacă putem elimina restul după al doilea termen al seriei rezultate.
0,0001<0.001. Следовательно, .