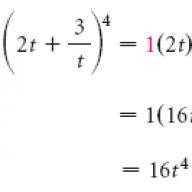วิธีแยกตัวประกอบตัวเลขเป็นผลคูณของตัวประกอบเฉพาะ ทวินามของนิวตันโดยใช้สัญกรณ์แฟกทอเรียล

พิจารณานิพจน์ต่อไปนี้ซึ่งมีกำลัง (a + b) n โดยที่ a + b คือทวินามใดๆ และ n คือจำนวนเต็ม

แต่ละนิพจน์เป็นพหุนาม คุณสามารถสังเกตเห็นคุณสมบัติในทุกสำนวน

1. ในแต่ละนิพจน์ มีคำศัพท์มากกว่าหนึ่งคำที่มากกว่าเลขชี้กำลัง n

2. ในแต่ละเทอม ผลรวมของกำลังจะเท่ากับ n นั่นคือ พลังที่ยกทวินามขึ้นมา

3. กำลังเริ่มต้นจากกำลังทวินาม n และลดลงไปทาง 0 เทอมสุดท้ายไม่มีตัวประกอบ a เทอมแรกไม่มีปัจจัย b นั่นคือ องศา b เริ่มต้นที่ 0 และเพิ่มเป็น n

4. ค่าสัมประสิทธิ์เริ่มต้นที่ 1 และเพิ่มขึ้นตามค่าที่กำหนดจนถึง "ครึ่งทาง" แล้วลดลงตามค่าเดิมกลับเป็น 1

มาดูค่าสัมประสิทธิ์ให้ละเอียดยิ่งขึ้น สมมติว่าเราต้องการหาค่าของ (a + b) 6 จากฟีเจอร์ที่เราเพิ่งสังเกตเห็น น่าจะมีสมาชิก 7 คนที่นี่
a 6 + c 1 a 5 b + c 2 a 4 b 2 + c 3 a 3 b 3 + c 4 a 2 b 4 + c 5 ab 5 + b 6 .
แต่เราจะกำหนดค่าของแต่ละสัมประสิทธิ์ได้อย่างไร c i ? เราสามารถทำได้สองวิธี วิธีแรกเกี่ยวข้องกับการเขียนสัมประสิทธิ์ในรูปสามเหลี่ยม ดังที่แสดงด้านล่าง สิ่งนี้เรียกว่า สามเหลี่ยมปาสคาล :


มีลักษณะเด่นหลายประการในรูปสามเหลี่ยม ค้นหาให้ได้มากที่สุด
คุณอาจพบวิธีเขียนชุดตัวเลขถัดไปโดยใช้ตัวเลขในบรรทัดด้านบน หน่วยต่างๆ จะตั้งอยู่ด้านข้างเสมอ จำนวนที่เหลือแต่ละตัวคือผลรวมของตัวเลขสองตัวที่อยู่เหนือตัวเลขนั้น ลองค้นหาค่าของนิพจน์ (a + b) 6 โดยเพิ่มบรรทัดต่อไปนี้ โดยใช้ฟีเจอร์ที่เราพบ:

เราเห็นสิ่งนั้นในบรรทัดสุดท้าย

ตัวเลขตัวแรกและตัวสุดท้าย 1 ;
ตัวเลขที่สองคือ 1 + 5 หรือ 6 ;
ตัวเลขที่สามคือ 5 + 10 หรือ 15 ;
ตัวเลขที่สี่คือ 10 + 10 หรือ 20 ;
ตัวเลขที่ห้าคือ 10 + 5 หรือ 15 - และ
ตัวเลขที่หกคือ 5 + 1 หรือ 6 .

ดังนั้นนิพจน์ (a + b) 6 จะเท่ากับ
(ก + ข) 6 = 1 เอ 6+ 6 ก 5 ข + 15 ก 4 ข 2 + 20 ก 3 ข 3 + 15 ก 2 ข 4 + 6 ประมาณ 5+ 1 ข 6.

หากต้องการยกกำลัง (a + b) 8 เราจะเพิ่มเส้นสองเส้นที่สามเหลี่ยมของ Pascal:

แล้ว
(ก + ข) 8 = ก 8 + 8a 7 ข + 28a 6 ข 2 + 56a 5 ข 3 + 70a 4 ข 4 + 56a 3 ข 5 + 28a 2 ข 6 + 8ab 7 + ข 8 .

เราสามารถสรุปผลลัพธ์ของเราได้ดังนี้

ทวินามของนิวตันโดยใช้สามเหลี่ยมปาสคาล

สำหรับทวินาม a+ b และจำนวนธรรมชาติใดๆ n
(a + b) n = c 0 a n b 0 + c 1 a n-1 b 1 + c 2 a n-2 b 2 + .... + c n-1 a 1 b n-1 + c n a 0 b n ,
โดยที่ตัวเลข c 0 , c 1 , c 2 ,...., c n-1 , c n นำมาจากอนุกรม (n + 1) ของสามเหลี่ยมปาสคาล

ตัวอย่างที่ 1ยกกำลัง: (u - v) 5 .

สารละลายเรามี (a + b)n โดยที่ a = u, b = -v และ n = 5 เราใช้แถวที่ 6 ของสามเหลี่ยมปาสคาล:
1 5 10 10 5 1
แล้วเราก็มี
(คุณ-วี) 5 = 5 = 1 (ยู)5+ 5 (ยู) 4 (-วี) 1 + 10 (ยู) 3 (-วี) 2 + 10 (ยู) 2 (-วี) 3 + 5 (ยู)(-วี) 4 + 1 (-v) 5 = คุณ 5 - 5u 4 v + 10u 3 v 2 - 10u 2 v 3 + 5uv 4 - v 5
โปรดทราบว่าสัญญาณของเงื่อนไขจะผันผวนระหว่าง + และ - เมื่อดีกรี -v เป็นเลขคี่ เครื่องหมายจะเป็น -

ตัวอย่างที่ 2ยกกำลัง: (2t + 3/t) 4 .

สารละลายเรามี (a + b)n โดยที่ a = 2t, b = 3/t และ n = 4 เราใช้แถวที่ 5 ของสามเหลี่ยมปาสคาล:
1 4 6 4 1
แล้วเราก็มี

การขยายทวินามโดยใช้ค่าแฟกทอเรียล

สมมติว่าเราต้องการหาค่าของ (a + b) 11 ข้อเสียของการใช้สามเหลี่ยมปาสคาลคือเราต้องคำนวณแถวก่อนหน้าของสามเหลี่ยมทั้งหมดเพื่อให้ได้อนุกรมที่ต้องการ วิธีการต่อไปนี้จะหลีกเลี่ยงปัญหานี้ นอกจากนี้ยังช่วยให้คุณค้นหาแถวที่ต้องการ เช่น แถวที่ 8 โดยไม่ต้องประเมินแถวอื่นๆ ทั้งหมด วิธีการนี้มีประโยชน์ในการคำนวณ สถิติ และการใช้งาน สัญกรณ์สัมประสิทธิ์ทวินาม .
เราสามารถกำหนดทวินามของนิวตันได้ดังนี้

ทวินามของนิวตันโดยใช้สัญกรณ์แฟกทอเรียล

สำหรับทวินามใดๆ (a + b) และจำนวนธรรมชาติใดๆ n
.

ทวินามของนิวตันสามารถพิสูจน์ได้โดยการเหนี่ยวนำทางคณิตศาสตร์ แสดงว่าเหตุใดจึงเรียกว่า สัมประสิทธิ์ทวินาม .

ตัวอย่างที่ 3ยกกำลัง: (x 2 - 2y) 5 .

สารละลายเรามี (a + b) n โดยที่ a = x 2 , b = -2y และ n = 5 จากนั้น เมื่อใช้ทวินามของนิวตัน เราจะได้


สุดท้าย (x 2 - 2y) 5 = x 10 - 10x 8 y + 40x 6 y 2 - 80x 4 y 3 + 80x 2 y 4 - 35y 5

ตัวอย่างที่ 4ยกกำลัง: (2/x + 3√x) 4.

สารละลายเรามี (a + b)n โดยที่ a = 2/x, b = 3√x และ n = 4 จากนั้น เมื่อใช้ทวินามของนิวตัน เราจะได้


สุดท้าย (2/x + 3√x ) 4 = 16/x 4 + 96/x 5/2 + 216/x + 216x 1/2 + 81x 2

การค้นหาสมาชิกที่เฉพาะเจาะจง

สมมติว่าเราต้องการกำหนดคำศัพท์หนึ่งหรือคำอื่นจากนิพจน์ วิธีการที่เราพัฒนาจะทำให้เราสามารถค้นหาคำนี้ได้โดยไม่ต้องคำนวณแถวทั้งหมดของสามเหลี่ยมปาสคาลหรือค่าสัมประสิทธิ์ก่อนหน้านี้ทั้งหมด

โปรดทราบว่าในทวินามของนิวตันให้เทอมที่ 1 แก่เรา เทอมที่ 2 ให้เราเทอมที่ 3 และอื่นๆ สามารถสรุปได้ดังนี้

การหาเทอม (k + 1)

(k + 1) เทอมของนิพจน์ (a + b) n คือ

ตัวอย่างที่ 5ค้นหาพจน์ที่ 5 ในนิพจน์ (2x - 5y) 6 .

สารละลายขั้นแรก โปรดทราบว่า 5 = 4 + 1 จากนั้น k = 4, a = 2x, b = -5y และ n = 6 จากนั้นเทอมที่ 5 ของนิพจน์จะเป็น

ตัวอย่างที่ 6ค้นหาพจน์ที่ 8 ในนิพจน์ (3x - 2) 10

สารละลายอันดับแรก เราสังเกตว่า 8 = 7 + 1 จากนั้น k = 7, a = 3x, b = -2 และ n = 10 จากนั้นพจน์ที่ 8 ของนิพจน์จะเป็น

จำนวนชุดย่อยทั้งหมด

สมมติว่าเซตหนึ่งมีวัตถุ n อัน จำนวนเซตย่อยที่มีองค์ประกอบ k คือ จำนวนชุดย่อยทั้งหมดของชุดคือจำนวนชุดย่อยที่มี 0 องค์ประกอบ เช่นเดียวกับจำนวนชุดย่อยที่มี 1 องค์ประกอบ และจำนวนชุดย่อยที่มี 2 องค์ประกอบ และอื่นๆ จำนวนสับเซตทั้งหมดของเซตที่มี n องค์ประกอบคือ
.
ทีนี้มาดูการยกกำลัง (1 + 1) n:

.
ดังนั้น. จำนวนเซ็ตย่อยทั้งหมดคือ (1 + 1) n หรือ 2 n เราได้พิสูจน์สิ่งต่อไปนี้แล้ว

จำนวนชุดย่อยทั้งหมด

จำนวนสับเซตทั้งหมดของเซตที่มี n องค์ประกอบคือ 2n

ตัวอย่างที่ 7เซต (A, B, C, D, E) มีเซตย่อยกี่เซต?

สารละลายเซตนี้มี 5 องค์ประกอบ ดังนั้นจำนวนเซตย่อยคือ 2 5 หรือ 32

ตัวอย่างที่ 8เครือร้านอาหารของ Wendy มีท็อปปิ้งแฮมเบอร์เกอร์ดังต่อไปนี้:
{ซอสมะเขือเทศ มัสตาร์ด มายองเนส มะเขือเทศ ผักกาดหอม หัวหอม เห็ด มะกอก ชีส}.
เวนดี้สามารถเสนอแฮมเบอร์เกอร์ได้กี่ประเภท ไม่รวมขนาดหรือปริมาณของแฮมเบอร์เกอร์

สารละลายท็อปปิ้งบนแฮมเบอร์เกอร์แต่ละชิ้นเป็นสมาชิกของเซ็ตย่อยของเซ็ตท็อปปิ้งที่เป็นไปได้ทั้งหมด และเซ็ตว่างเป็นเพียงแฮมเบอร์เกอร์ จำนวนแฮมเบอร์เกอร์ที่เป็นไปได้ทั้งหมดจะเท่ากับ

- ดังนั้น Wendy's จึงสามารถนำเสนอแฮมเบอร์เกอร์ที่แตกต่างกันได้ 512 แบบ

จำนวนธรรมชาติใดๆ สามารถสลายเป็นผลคูณของตัวประกอบเฉพาะได้ หากคุณไม่ชอบการจัดการกับจำนวนจำนวนมาก เช่น 5733 เรียนรู้วิธีแยกตัวประกอบเหล่านี้เป็นตัวประกอบเฉพาะ (ในกรณีนี้คือ 3 x 3 x 7 x 7 x 13) ปัญหาที่คล้ายกันมักพบในการเข้ารหัสซึ่งเกี่ยวข้องกับปัญหาความปลอดภัยของข้อมูล หากคุณยังไม่พร้อมที่จะสร้างระบบอีเมลที่ปลอดภัยของคุณเอง ให้เริ่มต้นด้วยการเรียนรู้วิธีแยกตัวเลขให้เป็นปัจจัยเฉพาะ

ขั้นตอน

ส่วนที่ 1

การหาปัจจัยเฉพาะ

1. เริ่มต้นด้วยหมายเลขเดิมเลือกจำนวนประกอบที่มากกว่า 3 การหาจำนวนเฉพาะไม่มีประโยชน์ เนื่องจากจะหารด้วยตัวมันเองและหนึ่งเท่านั้น

   • ตัวอย่าง: ลองแยกเลข 24 เป็นผลคูณของจำนวนเฉพาะกัน

2. ลองแยกตัวเลขนี้เป็นผลคูณของตัวประกอบสองตัวกันลองหาตัวเลขที่น้อยกว่าสองตัวที่มีผลคูณเท่ากับตัวเลขเดิม คุณสามารถใช้ตัวประกอบอะไรก็ได้ แต่การใช้จำนวนเฉพาะจะง่ายกว่า วิธีที่ดีวิธีหนึ่งคือลองหารจำนวนเดิมก่อนด้วย 2 จากนั้นด้วย 3 จากนั้นด้วย 5 และตรวจสอบว่าจำนวนเฉพาะใดที่หารลงตัวโดยไม่เหลือเศษ

   • ตัวอย่าง: หากคุณไม่ทราบตัวประกอบของเลข 24 ให้ลองหารมันเป็นจำนวนเฉพาะเล็กๆ ดังนั้นคุณจะพบว่าตัวเลขที่กำหนดหารด้วย 2: 24 = 2x12- นี่เป็นการเริ่มต้นที่ดี
   • เนื่องจาก 2 เป็นจำนวนเฉพาะ จึงเหมาะที่จะใช้แยกตัวประกอบเลขคู่

3. เริ่มสร้างแผนผังตัวคูณของคุณขั้นตอนง่ายๆ นี้จะช่วยให้คุณแยกตัวประกอบตัวเลขให้เป็นตัวประกอบเฉพาะได้ ในการเริ่มต้น ให้วาด "กิ่งก้าน" สองอันลงมาจากหมายเลขเดิม ในตอนท้ายของแต่ละสาขาให้เขียนปัจจัยที่คุณพบ

   • ตัวอย่าง:

4. แยกตัวประกอบสตริงตัวเลขต่อไปนี้ดูตัวเลขใหม่สองตัว (แถวที่สองของแผนผังตัวประกอบ) เป็นเลขเฉพาะทั้งคู่หรือเปล่า? ถ้าตัวใดตัวหนึ่งไม่ใช่จำนวนเฉพาะ ให้แยกตัวออกเป็นสองด้วย วาดกิ่งเพิ่มอีกสองกิ่งแล้วเขียนตัวประกอบใหม่สองตัวบนบรรทัดที่สามของต้นไม้

   • ตัวอย่าง: 12 ไม่ใช่จำนวนเฉพาะ จึงต้องแยกตัวประกอบ เราใช้ส่วนขยาย 12 = 2 x 6 และเขียนลงในบรรทัดที่สามของแผนผัง:
   • 2x6

5. ลงต้นไม้ต่อไปหากปัจจัยใหม่ตัวใดตัวหนึ่งกลายเป็นจำนวนเฉพาะ ให้วาด "กิ่งก้าน" จากนั้นเขียนตัวเลขเดียวกันที่ส่วนท้ายของตัวมัน จำนวนเฉพาะไม่ได้แยกตัวประกอบเป็นจำนวนที่น้อยกว่า ดังนั้นให้เลื่อนลงมาหนึ่งระดับ

   • ตัวอย่าง: 2 เป็นจำนวนเฉพาะ เพียงย้าย 2 จากบรรทัดที่สองไปยังบรรทัดที่สาม:
   • 2 2 6

6. แยกตัวประกอบตัวเลขต่อไปจนกว่าคุณจะเหลือเพียงจำนวนเฉพาะเท่านั้นตรวจสอบแต่ละบรรทัดใหม่ของต้นไม้ ถ้าตัวประกอบใหม่อย่างน้อยหนึ่งตัวไม่ใช่จำนวนเฉพาะ ให้แยกตัวประกอบแล้วเขียนบรรทัดใหม่ สุดท้ายก็จะเหลือเพียงจำนวนเฉพาะ

   • ตัวอย่าง: 6 ไม่ใช่จำนวนเฉพาะ จึงต้องแยกตัวประกอบด้วย ในขณะเดียวกัน 2 ก็เป็นจำนวนเฉพาะ และเรานำ 2 สองตัวขึ้นไปในระดับถัดไป:
   • 2 2 6
   • / / /\
   • 2 2 2 3

7. เขียนบรรทัดสุดท้ายเป็นผลคูณของตัวประกอบเฉพาะสุดท้ายก็จะเหลือเพียงจำนวนเฉพาะ เมื่อสิ่งนี้เกิดขึ้น การแยกตัวประกอบจะเสร็จสมบูรณ์ บรรทัดสุดท้ายคือชุดของจำนวนเฉพาะ ซึ่งผลคูณของจำนวนนั้นให้จำนวนเดิม

   • ตรวจสอบคำตอบของคุณ: คูณตัวเลขในบรรทัดสุดท้าย ผลลัพธ์ควรเป็นหมายเลขเดิม
   • ตัวอย่าง: แถวสุดท้ายของแผนผังตัวประกอบประกอบด้วยตัวเลข 2 และ 3 ตัวเลขทั้งสองนี้เป็นจำนวนเฉพาะ ดังนั้นการแยกตัวประกอบจึงเสร็จสมบูรณ์ ดังนั้นการสลายตัวของเลข 24 เป็นตัวประกอบเฉพาะจึงเป็นดังนี้: 24 = 2 x 2 x 2 x 3.
   • ลำดับของปัจจัยไม่สำคัญ ส่วนขยายสามารถเขียนเป็น 2 x 3 x 2 x 2 ได้ด้วย

8. หากต้องการ ให้ลดความซับซ้อนของคำตอบโดยใช้สัญลักษณ์ยกกำลังหากคุณคุ้นเคยกับการยกกำลัง คุณสามารถเขียนคำตอบในรูปแบบที่ง่ายกว่าได้ จำไว้ว่าฐานเขียนไว้ด้านล่าง และหมายเลขตัวยกจะแสดงจำนวนครั้งที่ฐานต้องคูณด้วยตัวมันเอง

   • ตัวอย่าง: ตัวเลข 2 ปรากฏในการสลายตัวที่พบ 2 x 2 x 2 x 3 กี่ครั้ง? สามครั้ง ดังนั้นนิพจน์ 2 x 2 x 2 สามารถเขียนเป็น 2 3 ได้ ในสัญกรณ์แบบง่ายที่เราได้รับ 2 3 x 3.

   ส่วนที่ 2

   การใช้การแยกตัวประกอบเฉพาะ

   1. หาตัวหารร่วมมากของตัวเลขสองตัว.ตัวหารร่วมมาก (GCD) ของตัวเลขสองตัวคือจำนวนสูงสุดที่หารทั้งสองตัวเลขโดยไม่ทิ้งเศษ ตัวอย่างด้านล่างแสดงวิธีใช้การแยกตัวประกอบเฉพาะเพื่อหาตัวประกอบร่วมที่ยิ่งใหญ่ที่สุดของตัวเลข 30 และ 36

      • ลองแยกตัวเลขทั้งสองให้เป็นตัวประกอบเฉพาะ. สำหรับเลข 30 ส่วนขยายคือ 2 x 3 x 5 จำนวน 36 จะถูกแยกตัวประกอบดังนี้: 2 x 2 x 3 x 3
      • เรามาค้นหาตัวเลขที่ปรากฏในส่วนขยายทั้งสองกัน ลองขีดฆ่าตัวเลขนี้ในทั้งสองรายการแล้วเขียนขึ้นบรรทัดใหม่ ตัวอย่างเช่น 2 เกิดขึ้นในสองส่วนขยาย ดังนั้นเราจึงเขียน 2 บนบรรทัดใหม่ จะได้ 30 = 2 x 3 x 5 และ 36 = 2 x 2 x 3 x 3
      • ทำซ้ำขั้นตอนนี้จนกว่าจะไม่มีปัจจัยทั่วไปเหลืออยู่ในการขยาย ทั้งสองรายการมีหมายเลข 3 ด้วย ดังนั้นคุณจึงสามารถเขียนขึ้นบรรทัดใหม่ได้ 2 และ 3 - หลังจากนั้น ให้เปรียบเทียบการขยายอีกครั้ง: 30 = 2 x 3 x 5 และ 36 = 2 x 2 x 3 x 3 อย่างที่คุณเห็น ไม่มีปัจจัยร่วมเหลืออยู่ในส่วนขยายเหล่านี้
      • หากต้องการหาตัวประกอบร่วมที่ยิ่งใหญ่ที่สุด คุณต้องหาผลคูณของตัวประกอบร่วมทั้งหมด ในตัวอย่างของเรา มันคือ 2 และ 3 ดังนั้น gcd คือ 2 x 3 = 6 - นี่คือจำนวนที่มากที่สุดที่สามารถหาร 30 และ 36 ได้โดยไม่เหลือเศษ

   2. การใช้ GCD จะทำให้เศษส่วนง่ายขึ้นหากคุณสงสัยว่าเศษส่วนสามารถลดลงได้ ให้ใช้ตัวประกอบร่วมที่ยิ่งใหญ่ที่สุด โดยใช้ขั้นตอนที่อธิบายไว้ข้างต้น ค้นหา gcd ของตัวเศษและส่วน จากนั้นให้หารทั้งเศษและส่วนของเศษส่วนด้วยจำนวนนั้น ผลลัพธ์ก็คือคุณจะได้เศษส่วนเท่ากันในรูปแบบที่ง่ายกว่า

      • ตัวอย่างเช่น ลองลดรูปเศษส่วน 30/36 กัน ตามที่เรากำหนดไว้ข้างต้น สำหรับ 30 และ 36 gcd คือ 6 ดังนั้นเราจึงหารทั้งเศษและส่วนด้วย 6:
      • 30 ۞ 6 = 5
      • 36 ۞ 6 = 6
      • 30 / 36 = 5 / 6

   3. ลองหาตัวคูณร่วมน้อยของตัวเลขสองตัวกันตัวคูณร่วมน้อย (LCM) ของตัวเลขสองตัวคือจำนวนที่น้อยที่สุดที่หารด้วยตัวเลขที่กำหนดทั้งสองจำนวนลงตัวโดยไม่เหลือเศษ ตัวอย่างเช่น LCM ของ 2 และ 3 คือ 6 เนื่องจากเป็นจำนวนที่น้อยที่สุดที่หารด้วย 2 และ 3 ลงตัว ด้านล่างนี้เป็นตัวอย่างการค้นหา LCM โดยใช้การแยกตัวประกอบเฉพาะ:

      • เริ่มจากการแยกตัวประกอบเฉพาะสองตัวกันก่อน ตัวอย่างเช่น สำหรับจำนวน 126 การแยกตัวประกอบสามารถเขียนเป็น 2 x 3 x 3 x 7 จำนวน 84 สามารถแยกตัวประกอบเป็น 2 x 2 x 3 x 7
      • ลองเปรียบเทียบดูว่าแต่ละปัจจัยปรากฏในส่วนขยายกี่ครั้ง เลือกรายการที่ตัวคูณปรากฏตามจำนวนครั้งสูงสุดแล้ววงกลม ตัวอย่างเช่น หมายเลข 2 ปรากฏหนึ่งครั้งในรายการสำหรับ 126 และสองครั้งในรายการสำหรับ 84 ดังนั้นคุณควรวงกลม 2x2ในรายการตัวคูณที่สอง
      • ทำซ้ำขั้นตอนนี้กับตัวคูณแต่ละตัว ตัวอย่างเช่น 3 เกิดขึ้นบ่อยกว่าในส่วนขยายแรก ดังนั้นคุณควรวงกลมไว้ 3x3- เลข 7 ปรากฏครั้งเดียวในทั้งสองรายการ ดังนั้นให้วงกลม 7 (ไม่สำคัญว่าจะอยู่ในรายการใด หากตัวคูณที่กำหนดปรากฏในทั้งสองรายการมีจำนวนครั้งเท่ากัน)
      • หากต้องการค้นหา LCM ให้คูณตัวเลขในวงกลมทั้งหมด ในตัวอย่างของเรา ตัวคูณร่วมน้อยของ 126 และ 84 คือ 2 x 2 x 3 x 3 x 7 = 252- นี่คือจำนวนที่น้อยที่สุดที่หารด้วย 126 และ 84 ลงตัวโดยไม่มีเศษ

   4. ใช้ LCM ในการบวกเศษส่วนเมื่อบวกเศษส่วนสองจำนวน คุณต้องนำมาหารด้วยตัวส่วนร่วม เมื่อต้องการทำเช่นนี้ ให้ค้นหา LCM ของตัวส่วนสองตัว จากนั้นคูณตัวเศษและส่วนของเศษส่วนแต่ละส่วนด้วยจำนวนจนตัวส่วนของเศษส่วนเท่ากับ LCM หลังจากนั้นคุณสามารถเพิ่มเศษส่วนได้

      • เช่น คุณต้องหาผลรวม 1/6 + 4/21
      • เมื่อใช้วิธีการข้างต้น คุณจะพบ LCM สำหรับ 6 และ 21 ซึ่งเท่ากับ 42
      • ลองแปลงเศษส่วน 1/6 เพื่อให้ตัวส่วนของมันเท่ากับ 42 ในการทำเช่นนี้คุณต้องหาร 42 ด้วย 6: 42 ÷ 6 = 7 ตอนนี้คูณตัวเศษและส่วนของเศษส่วนด้วย 7: 1/6 x 7/7 = 7/42
      • หากต้องการนำเศษส่วนที่สองมาหารด้วย 42 ให้หาร 42 ด้วย 21: 42 ÷ 21 = 2 คูณทั้งเศษและส่วนของเศษส่วนด้วย 2: 4 / 21 x 2 / 2 = 8 / 42
      • เมื่อเศษส่วนลดลงจนเหลือตัวส่วนเท่ากัน ก็จะบวกกันได้ง่ายๆ: 7/42 + 8/42 = 15/42

ในบทความนี้คุณจะพบข้อมูลที่จำเป็นทั้งหมดเพื่อตอบคำถาม วิธีแยกตัวประกอบจำนวนให้เป็นตัวประกอบเฉพาะ- ขั้นแรกให้แนวคิดทั่วไปเกี่ยวกับการสลายตัวของตัวเลขเป็นปัจจัยเฉพาะและให้ตัวอย่างของการสลายตัว ข้อมูลต่อไปนี้แสดงรูปแบบมาตรฐานของการแบ่งจำนวนตัวเลขให้เป็นตัวประกอบเฉพาะ หลังจากนั้นจะมีการกำหนดอัลกอริทึมสำหรับการแยกย่อยตัวเลขตามใจชอบให้เป็นปัจจัยเฉพาะและให้ตัวอย่างการแยกย่อยตัวเลขโดยใช้อัลกอริทึมนี้ นอกจากนี้ ยังมีการพิจารณาวิธีอื่นที่ช่วยให้คุณสามารถแยกตัวประกอบจำนวนเต็มขนาดเล็กให้เป็นตัวประกอบเฉพาะได้อย่างรวดเร็วโดยใช้การทดสอบการหารลงตัวและตารางสูตรคูณ

การนำทางหน้า

การแยกตัวประกอบตัวเลขให้เป็นตัวประกอบเฉพาะหมายความว่าอย่างไร?

ก่อนอื่น เรามาดูกันว่าปัจจัยสำคัญคืออะไร

เห็นได้ชัดว่าเนื่องจากมีคำว่า "ปัจจัย" ในวลีนี้ จึงมีผลคูณของตัวเลขจำนวนหนึ่ง และคำว่า "ง่าย" ที่เข้าเกณฑ์หมายความว่าแต่ละปัจจัยเป็นจำนวนเฉพาะ ตัวอย่างเช่น ในผลคูณของรูปแบบ 2·7·7·23 มีตัวประกอบเฉพาะสี่ตัว: 2, 7, 7 และ 23

การแยกตัวประกอบตัวเลขให้เป็นตัวประกอบเฉพาะหมายความว่าอย่างไร?

ซึ่งหมายความว่าตัวเลขนี้จะต้องแสดงเป็นผลคูณของตัวประกอบเฉพาะ และมูลค่าของผลิตภัณฑ์นี้จะต้องเท่ากับตัวเลขเดิม ตัวอย่างเช่น ลองพิจารณาผลคูณของจำนวนเฉพาะสามจำนวน 2, 3 และ 5 ซึ่งมีค่าเท่ากับ 30 ดังนั้นการสลายตัวของจำนวน 30 ให้เป็นตัวประกอบเฉพาะคือ 2·3·5 โดยปกติแล้ว การสลายตัวของตัวเลขให้เป็นตัวประกอบเฉพาะจะเขียนเป็นความเท่าเทียมกัน ในตัวอย่างของเรา มันจะเป็นดังนี้: 30=2·3·5 เราเน้นแยกกันว่าปัจจัยสำคัญในการขยายสามารถทำซ้ำได้ ตัวอย่างต่อไปนี้แสดงให้เห็นอย่างชัดเจน: 144=2·2·2·2·3·3 แต่การแทนค่าในรูปแบบ 45=3·15 ไม่ใช่การสลายตัวของตัวประกอบเฉพาะ เนื่องจากเลข 15 เป็นจำนวนประกอบ

คำถามต่อไปนี้เกิดขึ้น: “ตัวเลขใดที่สามารถแยกย่อยเป็นตัวประกอบเฉพาะได้”

ในการค้นหาคำตอบ เราขอเสนอเหตุผลดังต่อไปนี้ จำนวนเฉพาะตามคำนิยาม อยู่ในกลุ่มจำนวนที่มากกว่าหนึ่ง เมื่อพิจารณาข้อเท็จจริงนี้ และ อาจโต้แย้งได้ว่าผลคูณของตัวประกอบเฉพาะหลายตัวเป็นจำนวนเต็มบวกที่มากกว่า 1 ดังนั้น การแยกตัวประกอบจึงเกิดขึ้นเฉพาะกับจำนวนเต็มบวกที่มากกว่า 1 เท่านั้น

แต่จำนวนเต็มทั้งหมดที่มากกว่า 1 สามารถแยกตัวประกอบเป็นจำนวนเฉพาะได้หรือไม่?

เห็นได้ชัดเจนว่าไม่สามารถแยกตัวประกอบจำนวนเต็มเชิงเดี่ยวให้เป็นตัวประกอบเฉพาะได้ เนื่องจากจำนวนเฉพาะมีตัวประกอบบวกเพียงสองตัวเท่านั้น - ตัวหนึ่งและตัวมันเอง ดังนั้นจึงไม่สามารถแสดงเป็นผลคูณของจำนวนเฉพาะสองตัวขึ้นไปได้ ถ้าจำนวนเต็ม z สามารถแทนเป็นผลคูณของจำนวนเฉพาะ a และ b ได้ แนวคิดเรื่องการหารลงตัวจะทำให้เราสรุปได้ว่า z หารด้วยทั้ง a และ b ลงตัว ซึ่งเป็นไปไม่ได้เนื่องจากความเรียบง่ายของจำนวน z อย่างไรก็ตาม พวกเขาเชื่อว่าจำนวนเฉพาะใดๆ ก็คือการสลายตัวนั่นเอง

แล้วจำนวนประกอบล่ะ? จำนวนประกอบจะสลายตัวไปเป็นตัวประกอบเฉพาะ และจำนวนประกอบทั้งหมดมีการสลายตัวเช่นนั้นหรือไม่ ทฤษฎีบทพื้นฐานของเลขคณิตให้คำตอบที่ยืนยันกับคำถามจำนวนหนึ่งเหล่านี้ ทฤษฎีบทพื้นฐานของเลขคณิตระบุว่าจำนวนเต็ม a ใดๆ ที่มากกว่า 1 สามารถสลายตัวเป็นผลคูณของตัวประกอบเฉพาะ p 1, p 2, ..., p n และการสลายตัวจะมีรูปแบบ a = p 1 · p 2 · … · p n และการขยายตัวนี้จะไม่ซ้ำกัน ถ้าคุณไม่คำนึงถึงลำดับของปัจจัย

การแยกตัวประกอบมาตรฐานของจำนวนให้เป็นตัวประกอบเฉพาะ

ในการขยายจำนวน ตัวประกอบเฉพาะสามารถทำซ้ำได้ การทำซ้ำตัวประกอบเฉพาะสามารถเขียนให้กระชับยิ่งขึ้นได้โดยใช้ ปล่อยให้ในการสลายตัวของตัวเลข ตัวประกอบเฉพาะ p 1 เกิดขึ้น s 1 ครั้ง ตัวประกอบเฉพาะ p 2 – s 2 ครั้ง และต่อไปเรื่อยๆ p n – s n คูณ จากนั้นการแยกตัวประกอบเฉพาะของจำนวน a สามารถเขียนได้เป็น a=p 1 s 1 ·p 2 s 2 ·…·p n s n- การบันทึกรูปแบบนี้เรียกว่า การแยกตัวประกอบมาตรฐานของจำนวนให้เป็นตัวประกอบเฉพาะ.

ขอให้เรายกตัวอย่างการแบ่งแยกตามบัญญัติของตัวเลขให้เป็นปัจจัยเฉพาะ แจ้งให้เราทราบถึงการสลายตัว 609 840=2 2 2 2 3 3 5 7 11 11สัญกรณ์ตามรูปแบบบัญญัติมีรูปแบบ 609 840=2 4 3 2 5 7 11 2.

การแยกตัวประกอบตัวเลขตามรูปแบบบัญญัติให้เป็นตัวประกอบเฉพาะจะทำให้คุณสามารถค้นหาตัวหารทั้งหมดของตัวเลขและจำนวนตัวหารของตัวเลขได้

อัลกอริทึมในการแยกตัวเลขให้เป็นตัวประกอบเฉพาะ

เพื่อที่จะรับมือกับงานแยกย่อยตัวเลขให้เป็นตัวประกอบเฉพาะได้สำเร็จ คุณต้องมีความรู้เป็นอย่างดีเกี่ยวกับข้อมูลในบทความเรื่องจำนวนเฉพาะและจำนวนประกอบ

สาระสำคัญของกระบวนการสลายจำนวนเต็มบวก a ที่เกินกว่าหนึ่งนั้นชัดเจนจากการพิสูจน์ทฤษฎีบทพื้นฐานของเลขคณิต ประเด็นคือการหาตัวหารเฉพาะที่น้อยที่สุดตามลำดับ p 1, p 2, ..., p n ของตัวเลข a, a 1, a 2, ..., n-1 ซึ่งช่วยให้เราได้ชุดค่าที่เท่ากัน a=p 1 ·a 1 โดยที่ a 1 = a:p 1 , a=p 1 ·a 1 =p 1 ·p 2 ·a 2 โดยที่ a 2 =a 1:p 2 , …, a=p 1 ·p 2 ·…·p n ·a n โดยที่ a n =a n-1:p n เมื่อเราได้รับ n =1 แล้วความเท่าเทียมกัน a=p 1 ·p 2 ·…·p n จะทำให้เราได้การสลายตัวของจำนวน a ให้เป็นตัวประกอบเฉพาะที่ต้องการ ก็ควรสังเกตไว้ตรงนี้ด้วยว่า หน้า 1 ≤p 2 ≤p 3 ≤…≤p n.

ยังคงต้องหาวิธีค้นหาตัวประกอบเฉพาะที่เล็กที่สุดในแต่ละขั้นตอน และเราจะมีอัลกอริทึมในการแยกตัวเลขออกเป็นตัวประกอบเฉพาะ ตารางจำนวนเฉพาะจะช่วยเราค้นหาตัวประกอบเฉพาะ ให้เราแสดงวิธีใช้เพื่อให้ได้ตัวหารเฉพาะที่เล็กที่สุดของจำนวน z

เรานำจำนวนเฉพาะจากตารางจำนวนเฉพาะ (2, 3, 5, 7, 11 เป็นต้น) ตามลำดับ แล้วหารตัวเลขที่กำหนด z ด้วยตัวเลขเหล่านี้ จำนวนเฉพาะตัวแรกที่ z หารเท่ากันจะเป็นตัวหารเฉพาะที่น้อยที่สุด ถ้าเลข z เป็นจำนวนเฉพาะ ตัวหารเฉพาะที่น้อยที่สุดของมันจะเป็นตัวเลข z เอง ควรระลึกไว้ตรงนี้ว่า ถ้า z ไม่ใช่จำนวนเฉพาะ ตัวหารเฉพาะที่น้อยที่สุดก็จะไม่เกินจำนวน โดยที่มาจาก z ดังนั้น หากในบรรดาจำนวนเฉพาะที่ไม่เกิน ไม่มีตัวหารของจำนวน z ตัวเดียว เราก็สรุปได้ว่า z เป็นจำนวนเฉพาะ (ข้อมูลเพิ่มเติมเกี่ยวกับเรื่องนี้เขียนไว้ในส่วนทฤษฎีใต้หัวข้อ จำนวนนี้เป็นจำนวนเฉพาะหรือจำนวนประกอบ ).

ตัวอย่าง เราจะแสดงวิธีหาตัวหารเฉพาะที่น้อยที่สุดของจำนวน 87 เรามาเอาเลข 2 กันดีกว่า หาร 87 ด้วย 2 จะได้ 87:2=43 (เหลือ 1) (หากจำเป็น ดูบทความ) นั่นคือ เมื่อหาร 87 ด้วย 2 เศษคือ 1 ดังนั้น 2 จึงไม่ใช่ตัวหารของจำนวน 87 เรานำจำนวนเฉพาะตัวถัดไปจากตารางจำนวนเฉพาะ นี่คือเลข 3 หาร 87 ด้วย 3 เราจะได้ 87:3=29 ดังนั้น 87 หารด้วย 3 ลงตัว ดังนั้น เลข 3 จึงเป็นตัวหารเฉพาะที่น้อยที่สุดของเลข 87

โปรดทราบว่าในกรณีทั่วไป เพื่อแยกตัวประกอบจำนวน a ให้เป็นตัวประกอบเฉพาะ เราจำเป็นต้องมีตารางจำนวนเฉพาะที่มีจำนวนไม่ต่ำกว่า เราจะต้องอ้างอิงตารางนี้ในทุกขั้นตอน ดังนั้นเราจึงต้องมีตารางนี้อยู่ใกล้มือ ตัวอย่างเช่น หากต้องการแยกตัวประกอบจำนวน 95 ให้เป็นจำนวนเฉพาะ เราจำเป็นต้องมีเพียงตารางจำนวนเฉพาะที่มีค่าไม่เกิน 10 เท่านั้น (เนื่องจาก 10 มากกว่า ) และในการแยกย่อยเลข 846,653 คุณจะต้องมีตารางจำนวนเฉพาะมากถึง 1,000 อยู่แล้ว (เนื่องจาก 1,000 มากกว่า )

ขณะนี้เรามีข้อมูลเพียงพอที่จะจดบันทึกแล้ว อัลกอริธึมสำหรับการแยกตัวเลขให้เป็นตัวประกอบเฉพาะ- อัลกอริทึมสำหรับการสลายตัวของตัวเลข a มีดังนี้:

• เมื่อเรียงลำดับตัวเลขจากตารางจำนวนเฉพาะตามลำดับ เราจะพบตัวหารเฉพาะที่น้อยที่สุด p 1 ของจำนวน a หลังจากนั้นเราจะคำนวณ 1 =a:p 1 ถ้า 1 = 1 แสดงว่าจำนวน a เป็นจำนวนเฉพาะ และตัวมันเองก็คือการสลายตัวของตัวมันเองให้เป็นตัวประกอบเฉพาะ หาก 1 ไม่เท่ากับ 1 เราจะได้ a=p 1 ·a 1 และไปยังขั้นตอนถัดไป
• เราค้นหาตัวหารเฉพาะที่น้อยที่สุด p 2 ของตัวเลข a 1 โดยเราจะเรียงลำดับตัวเลขจากตารางจำนวนเฉพาะตามลำดับ โดยเริ่มจาก p 1 แล้วคำนวณ a 2 =a 1:p 2 ถ้า 2 =1 ดังนั้น การสลายตัวที่ต้องการของจำนวน a ให้เป็นตัวประกอบเฉพาะจะมีรูปแบบ a=p 1 ·p 2 หาก 2 ไม่เท่ากับ 1 เราจะได้ a=p 1 ·p 2 ·a 2 และไปยังขั้นตอนถัดไป
• เมื่อพิจารณาตัวเลขจากตารางจำนวนเฉพาะ เริ่มต้นด้วย p 2 เราจะพบตัวหารเฉพาะที่เล็กที่สุด p 3 ของจำนวน a 2 หลังจากนั้นเราจะคำนวณ 3 =a 2:p 3 ถ้า 3 =1 ดังนั้น การสลายตัวที่ต้องการของจำนวน a ให้เป็นตัวประกอบเฉพาะจะมีรูปแบบ a=p 1 ·p 2 ·p 3 หาก 3 ไม่เท่ากับ 1 เราจะได้ a=p 1 ·p 2 ·p 3 ·a 3 และไปยังขั้นตอนถัดไป
• เราค้นหาตัวหารเฉพาะที่น้อยที่สุด p n ของจำนวน a n-1 โดยการเรียงลำดับตามจำนวนเฉพาะ โดยเริ่มจาก p n-1 เช่นเดียวกับ a n =a n-1:p n และ a n เท่ากับ 1 ขั้นตอนนี้เป็นขั้นตอนสุดท้ายของอัลกอริทึม โดยเราจะได้การสลายตัวของจำนวน a ให้เป็นปัจจัยเฉพาะตามที่ต้องการ: a=p 1 ·p 2 ·…·p n

เพื่อความชัดเจน ผลลัพธ์ทั้งหมดที่ได้รับในแต่ละขั้นตอนของอัลกอริธึมในการแยกตัวเลขออกเป็นปัจจัยเฉพาะจะแสดงในรูปแบบของตารางต่อไปนี้ โดยที่ตัวเลข a, 1, 2, ..., n จะถูกเขียนตามลำดับ ในคอลัมน์ทางด้านซ้ายของเส้นแนวตั้งและทางด้านขวาของเส้น - ตัวหารเฉพาะที่เล็กที่สุดที่สอดคล้องกัน p 1, p 2, ..., p n

สิ่งที่เหลืออยู่คือการพิจารณาตัวอย่างบางส่วนของการประยุกต์ใช้อัลกอริธึมผลลัพธ์สำหรับการแยกตัวเลขออกเป็นปัจจัยเฉพาะ

ตัวอย่างของการแยกตัวประกอบเฉพาะ

ตอนนี้เราจะดูรายละเอียด ตัวอย่างการแยกตัวประกอบตัวเลขให้เป็นตัวประกอบเฉพาะ- เมื่อแยกย่อยเราจะใช้อัลกอริธึมจากย่อหน้าก่อนหน้า เริ่มจากกรณีง่าย ๆ แล้วค่อย ๆ ทำให้ซับซ้อนขึ้นเพื่อพบกับความแตกต่างที่เป็นไปได้ทั้งหมดที่เกิดขึ้นเมื่อแยกตัวเลขออกเป็นปัจจัยเฉพาะ

ตัวอย่าง.

แยกตัวประกอบของเลข 78 เป็นตัวประกอบเฉพาะ.

สารละลาย.

เราเริ่มค้นหาตัวหารเฉพาะตัวแรกที่เล็กที่สุด p 1 ของจำนวน a=78 เพื่อทำเช่นนี้ เราเริ่มเรียงลำดับจำนวนเฉพาะจากตารางจำนวนเฉพาะตามลำดับ เราเอาเลข 2 มาหาร 78 จะได้ 78:2=39 จำนวน 78 หารด้วย 2 โดยไม่มีเศษ ดังนั้น p 1 =2 จึงเป็นตัวหารเฉพาะตัวแรกที่พบของจำนวน 78 ในกรณีนี้ 1 =a:p 1 =78:2=39 เราก็มาถึงความเท่าเทียมกัน a=p 1 ·a 1 โดยมีรูปแบบ 78=2·39 แน่นอนว่า 1 =39 แตกต่างจาก 1 ดังนั้นเราจึงไปยังขั้นตอนที่สองของอัลกอริทึม

ตอนนี้เรากำลังมองหาตัวหารเฉพาะที่น้อยที่สุด p 2 ของจำนวน a 1 =39 เราเริ่มแจกแจงตัวเลขจากตารางจำนวนเฉพาะ โดยเริ่มจาก p 1 = 2 หาร 39 ด้วย 2 เราจะได้ 39:2=19 (เหลือ 1) เนื่องจาก 39 หารด้วย 2 ไม่ลงตัว ดังนั้น 2 จึงไม่ใช่ตัวหาร จากนั้นเรานำตัวเลขถัดไปจากตารางจำนวนเฉพาะ (หมายเลข 3) มาหาร 39 ด้วยจะได้ 39:3=13 ดังนั้น p 2 =3 จึงเป็นตัวหารเฉพาะที่น้อยที่สุดของจำนวน 39 ในขณะที่ 2 =a 1:p 2 =39:3=13 เรามีความเท่าเทียมกัน a=p 1 ·p 2 ·a 2 ในรูปแบบ 78=2·3·13 เนื่องจาก 2 =13 แตกต่างจาก 1 เราจึงไปยังขั้นตอนถัดไปของอัลกอริทึม

ตรงนี้เราต้องหาตัวหารเฉพาะที่น้อยที่สุดของจำนวน a 2 =13 ในการค้นหาตัวหารเฉพาะที่น้อยที่สุด p 3 ของจำนวน 13 เราจะเรียงลำดับตัวเลขจากตารางจำนวนเฉพาะตามลำดับ โดยเริ่มจาก p 2 = 3 จำนวน 13 หารด้วย 3 ไม่ลงตัว เนื่องจาก 13:3=4 (ส่วนที่เหลือ 1) และ 13 ก็หารด้วย 5, 7 และ 11 ไม่ลงตัว เนื่องจาก 13:5=2 (ส่วนที่เหลือ 3), 13:7=1 (พัก 6) และ 13:11=1 (พัก 2) จำนวนเฉพาะตัวถัดไปคือ 13 และ 13 หารลงตัวโดยไม่มีเศษ ดังนั้น p 3 ที่น้อยที่สุดของ 13 คือตัวมันเอง และ 3 =a 2:p 3 =13:13=1 เนื่องจาก 3 =1 ขั้นตอนของอัลกอริทึมนี้จึงเป็นขั้นตอนสุดท้าย และการสลายตัวของจำนวน 78 ที่ต้องการให้เป็นตัวประกอบเฉพาะจะมีรูปแบบ 78=2·3·13 (a=p 1 ·p 2 ·p 3 )

คำตอบ:

78=2·3·13.

ตัวอย่าง.

แสดงตัวเลข 83,006 เป็นผลคูณของตัวประกอบเฉพาะ

สารละลาย.

ในขั้นตอนแรกของอัลกอริทึมในการแยกตัวเลขออกเป็นปัจจัยเฉพาะ เราจะพบ p 1 =2 และ 1 =a:p 1 =83,006:2=41,503 โดยที่ 83,006=2·41,503

ในขั้นตอนที่ 2 เราจะพบว่า 2, 3 และ 5 ไม่ใช่ตัวหารเฉพาะของจำนวน a 1 = 41,503 แต่จำนวน 7 นั้นเป็น เนื่องจาก 41,503:7 = 5,929 เรามี p 2 =7, a 2 =a 1:p 2 =41,503:7=5,929 ดังนั้น 83,006=2 7 5 929.

ตัวหารเฉพาะที่น้อยที่สุดของจำนวน a 2 = 5 929 คือหมายเลข 7 เนื่องจาก 5 929:7 = 847 ดังนั้น p 3 =7, a 3 =a 2:p 3 =5 929:7 = 847 โดยที่ 83 006 = 2·7·7·847

ต่อไปเราจะพบว่าตัวหารเฉพาะที่น้อยที่สุด p 4 ของจำนวน a 3 =847 เท่ากับ 7 จากนั้น 4 =a 3:p 4 =847:7=121 ดังนั้น 83 006=2·7·7·7·121

ตอนนี้เราพบตัวหารเฉพาะที่น้อยที่สุดของจำนวน a 4 =121 มันคือจำนวน p 5 =11 (เนื่องจาก 121 หารด้วย 11 ลงตัวและหารด้วย 7 ไม่ลงตัว) จากนั้น 5 =a 4:p 5 =121:11=11 และ 83 006=2·7·7·7·11·11

สุดท้าย ตัวหารเฉพาะที่น้อยที่สุดของจำนวน a 5 =11 ก็คือจำนวน p 6 =11 จากนั้น 6 =a 5:p 6 =11:11=1 เนื่องจาก 6 =1 ขั้นตอนของอัลกอริธึมในการแยกตัวเลขออกเป็นปัจจัยเฉพาะจึงเป็นขั้นตอนสุดท้าย และการสลายตัวที่ต้องการจะมีรูปแบบ 83 006 = 2·7·7·7·11·11

ผลลัพธ์ที่ได้สามารถเขียนเป็นการสลายตัวตามบัญญัติของจำนวนให้เป็นตัวประกอบเฉพาะ 83 006 = 2·7 3 ·11 2

คำตอบ:

83 006=2 7 7 7 11 11=2 7 3 11 2 991 เป็นจำนวนเฉพาะ จริงๆ แล้ว มันไม่มีตัวหารเฉพาะตัวเดียวที่ไม่เกิน ( สามารถประมาณได้ประมาณว่า เนื่องจากเห็นได้ชัดว่า 991<40 2 ), то есть, наименьшим делителем числа 991 является оно само. Тогда p 3 =991 и a 3 =a 2:p 3 =991:991=1 . Следовательно, искомое разложение числа 897 924 289 на простые множители имеет вид 897 924 289=937·967·991 .

คำตอบ:

897 924 289 = 937 967 991 .

การใช้การทดสอบการหารลงตัวสำหรับการแยกตัวประกอบเฉพาะ

ในกรณีง่ายๆ คุณสามารถแยกตัวเลขออกเป็นปัจจัยเฉพาะได้โดยไม่ต้องใช้อัลกอริธึมการแยกย่อยจากย่อหน้าแรกของบทความนี้ ถ้าตัวเลขไม่มาก เมื่อจะแยกย่อยเป็นตัวประกอบเฉพาะ ก็มักจะเพียงพอที่จะทราบสัญญาณของการหารลงตัว ลองยกตัวอย่างเพื่อความกระจ่าง

เช่น เราต้องแยกตัวประกอบเลข 10 ให้เป็นตัวประกอบเฉพาะ จากตารางสูตรคูณ เรารู้ว่า 2·5=10 และตัวเลข 2 และ 5 เป็นจำนวนเฉพาะ ดังนั้นการแยกตัวประกอบเฉพาะของตัวเลข 10 จึงดูเหมือน 10=2·5

ตัวอย่างอื่น. เมื่อใช้ตารางสูตรคูณ เราจะแยกตัวประกอบของตัวเลข 48 ให้เป็นตัวประกอบเฉพาะ เรารู้ว่าหกคือแปด - สี่สิบแปดนั่นคือ 48 ​​= 6·8 อย่างไรก็ตาม ทั้ง 6 และ 8 ไม่ใช่จำนวนเฉพาะ แต่เรารู้ว่าสามสองตัวคือหก และสี่สองตัวคือแปด นั่นคือ 6=2·3 และ 8=2·4 จากนั้น 48=6·8=2·3·2·4. ที่ต้องจำไว้ว่าสองเท่าคือสี่ จากนั้นเราจะได้การสลายตัวที่ต้องการเป็นตัวประกอบเฉพาะ 48 = 2·3·2·2·2 มาเขียนส่วนขยายนี้ในรูปแบบมาตรฐาน: 48=2 4 ·3

แต่เมื่อนำจำนวน 3,400 ไปแยกตัวประกอบเป็นจำนวนเฉพาะ คุณสามารถใช้เกณฑ์การหารลงตัวได้ สัญญาณของการหารด้วย 10 ลงตัว, 100 ทำให้เราสามารถระบุได้ว่า 3,400 หารด้วย 100 ลงตัว โดยที่ 3,400=34·100 และ 100 หารด้วย 10 ลงตัว โดยที่ 100=10·10 ดังนั้น 3,400=34·10·10 และจากการทดสอบการหารด้วย 2 ลงตัว เราสามารถพูดได้ว่าตัวประกอบ 34, 10 และ 10 แต่ละตัวหารด้วย 2 ลงตัว เราจะได้ 3 400=34 10 10=2 17 2 5 2 5- ปัจจัยทั้งหมดในการขยายผลลัพธ์นั้นเรียบง่าย ดังนั้นการขยายนี้จึงเป็นที่ต้องการ สิ่งที่เหลืออยู่คือการจัดเรียงปัจจัยใหม่เพื่อให้เรียงลำดับจากน้อยไปหามาก: 3 400 = 2·2·2·5·5·17 ให้เราเขียนการแบ่งแยกตามรูปแบบบัญญัติของจำนวนนี้ให้เป็นตัวประกอบเฉพาะ: 3 400 = 2 3 ·5 2 ·17

เมื่อแยกตัวเลขที่กำหนดให้เป็นตัวประกอบเฉพาะ คุณสามารถใช้ทั้งเครื่องหมายของการหารลงตัวและตารางสูตรคูณตามลำดับ ลองจินตนาการว่าเลข 75 เป็นผลคูณของตัวประกอบเฉพาะ การทดสอบการหารด้วย 5 ลงตัวทำให้เราบอกได้ว่า 75 หารด้วย 5 ลงตัว และเราจะได้ 75 = 5·15 และจากตารางสูตรคูณ เราทราบว่า 15=3·5 ดังนั้น 75=5·3·5 นี่คือการสลายตัวที่จำเป็นของเลข 75 ให้กลายเป็นตัวประกอบเฉพาะ

บรรณานุกรม.

• วิเลนคิน เอ็น.ยา. และอื่น ๆ คณิตศาสตร์ ชั้นประถมศึกษาปีที่ 6: หนังสือเรียนสำหรับสถานศึกษาทั่วไป
• วิโนกราดอฟ ไอ.เอ็ม. พื้นฐานของทฤษฎีจำนวน
• มิเคโลวิช ช.เอช. ทฤษฎีจำนวน
• Kulikov L.Ya. และอื่น ๆ รวบรวมปัญหาพีชคณิตและทฤษฎีจำนวน: หนังสือเรียนสำหรับนักศึกษาวิชาฟิสิกส์และคณิตศาสตร์ เฉพาะทางของสถาบันการสอน

กรณีพิเศษของซีรีส์ Taylor สำหรับ x 0 =0

nมาเรียกตัวเองกันดีกว่าใกล้ แมคคลอริน สำหรับฟังก์ชั่นฉ(x).

ลองหาการสลายตัวของบางส่วน ระดับประถมศึกษาฟังก์ชั่นในซีรีส์ Maclaurin

ตัวอย่างที่ 23

.

สารละลาย.

เพื่อแก้ปัญหาเราจะใช้อัลกอริทึมที่กำหนดไว้ข้างต้น เนื่องจากจำเป็นต้องขยายฟังก์ชันเป็นซีรีส์ Maclaurin ดังนั้นเราจะมองหาส่วนขยายในบริเวณใกล้เคียงจุด เอ็กซ์ 0 = 0.

ลองหาค่าของฟังก์ชัน ณ จุดนั้นกัน เอ็กซ์ 0 =0, ฟังก์ชันอนุพันธ์สูงถึง ป-ลำดับที่และค่าของพวกเขาที่ เอ็กซ์ 0 = 0:

ให้เราเขียนชุด Maclaurin อย่างเป็นทางการโดยใช้สูตร

โปรดทราบว่าเราได้รับ rad สำหรับกำลังคี่ เนื่องจากค่าสัมประสิทธิ์สำหรับกำลังคู่ (เมื่อ ป- เลขคู่) มีค่าเท่ากับศูนย์

ให้เราค้นหาขอบเขตของการบรรจบกันของซีรีย์ผลลัพธ์ สำหรับสิ่งนี้ เรารวบรวมชุดของค่าสัมบูรณ์ของเงื่อนไขของซีรีย์:

แล้วติดป้ายดาล็องแบร์ไว้

เนื่องจากค่าของขีดจำกัดไม่ได้ขึ้นอยู่กับ เอ็กซ์และน้อยกว่าหนึ่งสำหรับสิ่งใดๆ เอ็กซ์จากนั้นอนุกรมจะลู่เข้าหากันสำหรับค่าทั้งหมด ซึ่งหมายความว่าช่วงของการลู่เข้าของอนุกรมนั้นเท่ากับ เอ็กซ์(–,+).

ตรวจสอบว่าตรงตามเงื่อนไขเพียงพอหรือไม่ เห็นได้ชัดว่า

สำหรับ ป= 0,1,2,... และสำหรับค่าใดๆ เอ็กซ์,

ซึ่งหมายความว่าฟังก์ชันนี้จะถูกขยายเป็นอนุกรม Maclaurin บนแกนตัวเลขทั้งหมด เช่น

ที่ เอ็กซ์(–,+).

ในตัวอย่างที่พิจารณา เพื่อกำหนดค่าสัมประสิทธิ์การขยายตัวของฟังก์ชันในอนุกรมกำลังใกล้กับจุดหนึ่ง เอ็กซ์ 0 =0 เราสร้างความแตกต่างให้กับฟังก์ชันอย่างต่อเนื่องจนกระทั่งได้สูตรมา ป-อนุพันธ์ลำดับที่ และหาค่าของอนุพันธ์ ณ จุดที่กำหนด แล้วพวกเขาก็พบว่าเพื่ออะไร เอ็กซ์เป็นไปตามเงื่อนไขที่เพียงพอสำหรับการสลายตัวของฟังก์ชันในชุดข้อมูล ขั้นตอนเหล่านี้มักนำไปสู่การคำนวณที่ยุ่งยาก ปัญหาเหล่านี้บางครั้งสามารถหลีกเลี่ยงได้โดยใช้ คำแถลงที่ การขยายฟังก์ชันไปสู่อนุกรมกำลังที่ได้รับไม่ว่าจะด้วยวิธีใดก็ตามจะเป็นการขยายไปสู่อนุกรมเทย์เลอร์ดังนั้น เพื่อที่จะขยายฟังก์ชันไปเป็นอนุกรมกำลัง เราสามารถใช้ส่วนขยายที่ทราบอยู่แล้วของฟังก์ชันพื้นฐาน นั่นคืออนุกรม Maclaurin โดยประยุกต์กฎการบวก การคูณอนุกรม และทฤษฎีบทเกี่ยวกับการอินทิเกรตและการหาอนุพันธ์ของฟังก์ชันเหล่านั้น ซีรีย์พาวเวอร์

เช่น การขยายฟังก์ชัน ฉ(x)= เพราะ x สามารถหาได้โดยการแยกความแตกต่างแบบเทอมต่อเทอมของการขยายอนุกรม Maclaurin ของฟังก์ชัน ฉ(x) = บาป x.

ที่ เอ็กซ์(–,+).

ในทำนองเดียวกัน การใช้อัลกอริธึมการขยายและทฤษฎีบทเกี่ยวกับการอินทิเกรตและการหาความแตกต่างของอนุกรมกำลัง เราสามารถรับการขยายอนุกรม Maclaurin ของฟังก์ชันพื้นฐานต่อไปนี้ได้

ที่ เอ็กซ์(–,+);

จถ้า t≥.0 หรือ t -1 แล้วบริเวณของการบรรจบกัน x (-1;1),

จถ้า–1< ต<0 , แล้วบริเวณลู่เข้าหากัน x (-1;1].

การสลายตัวนี้เรียกว่า อนุกรมทวินามโดยเฉพาะสมมติในการขยายตัวครั้งล่าสุด ต= –1, เราได้รับ

, เอ็กซ์ (-1;1).

เข้ามาแทนที่ในส่วนขยายนี้ เอ็กซ์ถึงการแสดงออก (- เอ็กซ์), เราได้รับ

, ที่ เอ็กซ์ (–1;1).

การใช้ทฤษฎีบทเกี่ยวกับการอินทิเกรตอนุกรมกำลังและนำไปใช้กับการขยายฟังก์ชันอนุกรมแมคลอริน
, เราได้รับ

ที่ เอ็กซ์ (–1;1].

การแทนที่ฟังก์ชันในส่วนขยาย
ตัวแปร เอ็กซ์ถึงการแสดงออก และบูรณาการ เราก็ได้

ที่ เอ็กซ์ [–1;1].

โดยใช้ อนุกรมทวินาม–การขยายฟังก์ชันชุด Maclaurin
สมมติว่า
, แทนที่ เอ็กซ์ถึงการแสดงออก
และบูรณาการ เราก็ได้

ที่ เอ็กซ์ (–1;1).

ตัวอย่างที่ 24

ใช้ส่วนขยายที่รู้จัก เพื่อขยายฟังก์ชันเป็นซีรีส์ Maclaurin
.

สารละลาย

จำเป็นต้องค้นหาส่วนขยายของฟังก์ชันในซีรีส์ Maclaurin เช่น ในชุดกำลังของกำลัง เอ็กซ์- เราจะใช้ส่วนขยาย

ที่ ที  (–1;1].

เชื่อ ที = x 2 , เราได้รับ

การขยายนี้จะมีผลเมื่อใด
, ที่ไหน
แล้วจึงเกิดบริเวณบรรจบกัน
.

ดังนั้น,

คูณความเท่ากันทั้งสองข้างด้วย เอ็กซ์, เราได้รับ

ที่ เอ็กซ์ [–1;1].

ปตัวอย่างที่ 25

ใช้การขยายที่รู้จัก เพื่อขยายฟังก์ชัน
ในชุดเทย์เลอร์ในบริเวณใกล้เคียงจุดหนึ่ง เอ็กซ์ 0 =1.

สารละลาย.

มีความจำเป็นต้องได้รับการขยายฟังก์ชันให้เป็นซีรีส์ Taylor ในบริเวณใกล้เคียงกับจุดนั้น เอ็กซ์ 0 = 1, เหล่านั้น. ตามองศา ( เอ็กซ์–1).

เราจะใช้ส่วนขยาย

ที่ ที  (-1;1).

เพื่อให้ได้มาซึ่งการขยายฟังก์ชันนี้ในด้านกำลัง ( เอ็กซ์–1) เรามาแนะนำตัวแปรใหม่กันดีกว่า ที= x–1, แล้ว x=ที + 1. ลองแปลงฟังก์ชันนี้เป็นตัวแปรใหม่กันเถอะ x=ที + 1:

สมมติว่าอยู่ในส่วนขยายที่รู้จักแทน ทีเราได้นิพจน์และการคูณตัวเลข

ที่  (-1;1).

สมมติว่าเกิดการขยายตัว ที = x–1, กลับไปที่ตัวแปรเดิมกันเถอะ เอ็กซ์และเราได้การขยายฟังก์ชันนี้เป็นอนุกรมกำลังในหน่วยกำลัง ( เอ็กซ์-1):

การขยายนี้ใช้ได้ภายใต้เงื่อนไข
, ที่ไหน
.

ดังนั้นเราจึงได้การสลายตัว

ที่
.

ตัวอย่างที่ 26

ขยายฟังก์ชัน
เข้าสู่อนุกรมกำลัง ณ จุดนั้น
.

สารละลาย.

มาแปลงฟังก์ชันนี้โดยใช้คุณสมบัติของลอการิทึม:

การใช้ส่วนขยายที่รู้จัก

ที่ ที  (–1;1].

ลองหาส่วนขยายของฟังก์ชันกัน
, เชื่อ ที= 2x, และฟังก์ชั่น
สมมติว่า ที= –x:

การขยายมีผลที่ 2 เอ็กซ์  (–1;1), เหล่านั้น. ที่
.

เช่นเดียวกัน,

และการขยายนั้นใช้ได้สำหรับ (- เอ็กซ์)  (–1;1) เช่น ที่ เอ็กซ์  (–1;1).

อนุกรมกำลังสามารถเพิ่มได้ทีละเทอมและคูณด้วยตัวเลข ซึ่งหมายถึง

นอกจากนี้ ส่วนขยายนี้ใช้ได้กับภูมิภาคลู่ทั่วไป เช่น ที่
.

ปตัวอย่างที่ 27

ขยายฟังก์ชันในชุด Maclaurin
.

สารละลาย.

มาแปลงฟังก์ชันกันดีกว่า

.

การใช้การขยายฟังก์ชันซีรีส์ Maclaurin ที่รู้จักกันดี ที่=(1+ ที) ม , เชื่อ
และ
, เราได้รับ

อนุกรมทวินามที่ใช้ที่
มีพื้นที่บรรจบกัน ที  (-1;1] ดังนั้น การขยายผลลัพธ์จึงใช้ได้สำหรับ
, ที่ไหน
,
.

ดังนั้น,
ที่
.

หากฟังก์ชัน f(x) มีอนุพันธ์ของลำดับทั้งหมดในช่วงเวลาหนึ่งที่มีจุด a แสดงว่าสามารถใช้สูตร Taylor ได้:
,
ที่ไหน ร– ที่เรียกว่าระยะเศษหรือเศษของอนุกรม สามารถประมาณได้โดยใช้สูตรลากรองจ์:
โดยที่ตัวเลข x อยู่ระหว่าง x และ a

กฎสำหรับการเข้าฟังก์ชั่น:

หากเพื่อคุณค่าบางอย่าง เอ็กซ์ ร→0 ณ n→∞ จากนั้นในขีดจำกัด สูตรเทย์เลอร์จะลู่เข้าหากันสำหรับค่านี้ เทย์เลอร์ซีรีส์:
,
ดังนั้น ฟังก์ชัน f(x) สามารถขยายเป็นอนุกรม Taylor ที่จุด x ที่อยู่ระหว่างการพิจารณาได้ ถ้า:
1) มีอนุพันธ์ของคำสั่งซื้อทั้งหมด
2) ซีรีย์ที่สร้างขึ้นมาบรรจบกัน ณ จุดนี้

เมื่อ a = 0 เราจะได้อนุกรมที่เรียกว่า ใกล้แมคคลอริน:
,
การขยายฟังก์ชันที่ง่ายที่สุด (ระดับประถมศึกษา) ในซีรี่ส์ Maclaurin:
ฟังก์ชันเลขชี้กำลัง
, R=∞
ฟังก์ชันตรีโกณมิติ
, R=∞
, R=∞
, (-π/2< x < π/2), R=π/2
ฟังก์ชัน actgx จะไม่ขยายกำลังของ x เพราะ CTG0=∞
ฟังก์ชันไฮเปอร์โบลิก


ฟังก์ชันลอการิทึม
, -1
อนุกรมทวินาม
.

ตัวอย่างหมายเลข 1 ขยายฟังก์ชันเป็นอนุกรมกำลัง ฉ(x)= 2x.
สารละลาย- ให้เราหาค่าของฟังก์ชันและอนุพันธ์ของมันที่ เอ็กซ์=0
ฉ(x) = 2x, ฉ( 0) = 2 0 =1;
ฉ"(x) = 2x ln2, ฉ"( 0) = 2 0 ln2= ln2;
ฉ""(x) = 2xใน 2 2, ฉ""( 0) = 2 0 อิน 2 2= อิน 2 2;
…
ฉ(n)(x) = 2x ln n 2, ฉ(n)( 0) = 2 0 ln n 2=ล n 2.
เราได้รับค่าอนุพันธ์ที่ได้รับมาแทนค่าที่ได้รับเป็นสูตรอนุกรมของ Taylor:

รัศมีของการบรรจบกันของอนุกรมนี้เท่ากับอนันต์ ดังนั้นส่วนขยายนี้ใช้ได้สำหรับ -∞<x<+∞.

ตัวอย่างหมายเลข 2 เขียนอนุกรมเทย์เลอร์ด้วยกำลัง ( เอ็กซ์+4) สำหรับฟังก์ชัน ฉ(x)=จ x.
สารละลาย- ค้นหาอนุพันธ์ของฟังก์ชัน e xและคุณค่าของมัน ณ จุดนั้น เอ็กซ์=-4.
ฉ(x)= อี x, ฉ(-4) = อี -4 ;
ฉ"(x)= อี x, ฉ"(-4) = อี -4 ;
ฉ""(x)= อี x, ฉ""(-4) = อี -4 ;
…
ฉ(n)(x)= อี x, ฉ(n)( -4) = อี -4 .
ดังนั้น อนุกรม Taylor ที่ต้องการของฟังก์ชันจึงมีรูปแบบดังนี้

ส่วนขยายนี้ใช้ได้กับ -∞ เช่นกัน<x<+∞.

ตัวอย่างหมายเลข 3 ขยายฟังก์ชัน ฉ(x)=ล xในซีรีส์ที่มีอำนาจ ( เอ็กซ์- 1),
(เช่น ในชุดเทย์เลอร์ในบริเวณใกล้จุดนั้น) เอ็กซ์=1).
สารละลาย- ค้นหาอนุพันธ์ของฟังก์ชันนี้
ฉ(x)=lnx , , , ,

ฉ(1)=ln1=0, ฉ"(1)=1, ฉ""(1)=-1, ฉ"""(1)=1*2,..., ฉ (n) =(- 1) n-1 (n-1)!
เมื่อแทนค่าเหล่านี้ลงในสูตรเราจะได้ซีรีย์ Taylor ที่ต้องการ:

เมื่อใช้การทดสอบของดาล็องแบร์ ​​คุณจะสามารถตรวจสอบได้ว่าอนุกรมมาบรรจบกันที่ ½x-1½<1 . Действительно,

อนุกรมมาบรรจบกันถ้า ½ เอ็กซ์- 1½<1, т.е. при 0<x<2. При เอ็กซ์=2 เราได้รับอนุกรมแบบสลับที่ตรงตามเงื่อนไขของเกณฑ์ของไลบ์นิซ เมื่อ x=0 ฟังก์ชันไม่ได้ถูกกำหนดไว้ ดังนั้น พื้นที่ของการบรรจบกันของอนุกรมเทย์เลอร์คือช่วงครึ่งเปิด (0;2)

ตัวอย่างหมายเลข 4 ขยายฟังก์ชันเป็นอนุกรมกำลัง
สารละลาย- ในส่วนขยาย (1) เราแทนที่ x ด้วย -x 2 เราจะได้:
, -∞

ตัวอย่างหมายเลข 5 ขยายฟังก์ชันในชุด Maclaurin .
สารละลาย- เรามี
ใช้สูตร (4) เราสามารถเขียนได้:

การแทนที่ –x แทนที่จะเป็น x ในสูตร เราจะได้:

จากตรงนี้ เราจะพบว่า: ln(1+x)-ln(1-x) = -
เราได้รับการเปิดวงเล็บ จัดเรียงเงื่อนไขของซีรี่ส์ใหม่และนำเงื่อนไขที่คล้ายกันมาใช้
- ชุดนี้มาบรรจบกันในช่วงเวลา (-1;1) เนื่องจากได้มาจากสองชุด ซึ่งแต่ละชุดมาบรรจบกันในช่วงเวลานี้

ความคิดเห็น .
สามารถใช้สูตร (1)-(5) เพื่อขยายฟังก์ชันที่เกี่ยวข้องให้เป็นอนุกรม Taylor ได้ เช่น สำหรับการขยายฟังก์ชันด้วยกำลังจำนวนเต็มบวก ( ฮา- ในการทำเช่นนี้ จำเป็นต้องทำการแปลงที่เหมือนกันบนฟังก์ชันที่กำหนดเพื่อให้ได้ฟังก์ชันใดฟังก์ชันหนึ่ง (1)-(5) ซึ่งแทน เอ็กซ์ต้นทุน k( ฮา) m โดยที่ k เป็นจำนวนคงที่ m เป็นจำนวนเต็มบวก การเปลี่ยนแปลงตัวแปรมักจะสะดวก ที=ฮาและขยายฟังก์ชันผลลัพธ์โดยคำนึงถึง t ในชุด Maclaurin

วิธีการนี้อิงตามทฤษฎีบทเรื่องความเป็นเอกลักษณ์ของการขยายตัวของฟังก์ชันในอนุกรมกำลัง แก่นแท้ของทฤษฎีบทนี้คือว่าในย่านใกล้เคียงจุดเดียวกัน ไม่สามารถรับอนุกรมกำลังที่แตกต่างกันสองชุดที่จะมาบรรจบกันเป็นฟังก์ชันเดียวกันได้ ไม่ว่าจะขยายด้วยวิธีใดก็ตาม

ตัวอย่างหมายเลข 5a ขยายฟังก์ชันในชุด Maclaurin และระบุขอบเขตของการบรรจบกัน
สารละลาย. ก่อนอื่นเราหา 1-x-6x 2 =(1-3x)(1+2x) , .
ถึงระดับประถมศึกษา:

เศษส่วน 3/(1-3x) ถือได้ว่าเป็นผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุดโดยมีตัวส่วนของ 3x ถ้า |3x|< 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

โดยมีขอบเขตบรรจบกัน |x|< 1/3.

ตัวอย่างหมายเลข 6 ขยายฟังก์ชันออกเป็นอนุกรม Taylor ใกล้กับจุด x = 3
สารละลาย- ปัญหานี้สามารถแก้ไขได้เช่นเดิมโดยใช้คำจำกัดความของอนุกรม Taylor ซึ่งเราต้องค้นหาอนุพันธ์ของฟังก์ชันและค่าของมันที่ เอ็กซ์=3. อย่างไรก็ตาม การใช้ส่วนขยายที่มีอยู่จะง่ายกว่า (5):
=
อนุกรมผลลัพธ์มาบรรจบกันที่หรือ –3

ตัวอย่างหมายเลข 7 เขียนอนุกรมเทย์เลอร์ด้วยกำลัง (x -1) ของฟังก์ชัน ln(x+2)
สารละลาย.


อนุกรมนี้มาบรรจบกันที่ หรือ -2< x < 5.

ตัวอย่างหมายเลข 8 ขยายฟังก์ชัน f(x)=sin(πx/4) ให้เป็นอนุกรมเทย์เลอร์ในบริเวณใกล้กับจุด x =2
สารละลาย- มาแทนที่กัน t=x-2:

เมื่อใช้ส่วนขยาย (3) ซึ่งเราแทนที่ π / 4 t แทน x เราจะได้:

อนุกรมผลลัพธ์มาบรรจบกันกับฟังก์ชันที่กำหนดที่ -∞< π / 4 t<+∞, т.е. при (-∞ดังนั้น,
, (-∞

การคำนวณโดยประมาณโดยใช้อนุกรมกำลัง

อนุกรมกำลังใช้กันอย่างแพร่หลายในการคำนวณโดยประมาณ ด้วยความช่วยเหลือของพวกเขา คุณสามารถคำนวณค่าของราก ฟังก์ชันตรีโกณมิติ ลอการิทึมของตัวเลข และอินทิกรัลจำกัดด้วยความแม่นยำที่กำหนด อนุกรมยังใช้เมื่อทำการอินทิเกรตสมการเชิงอนุพันธ์อีกด้วย
พิจารณาการขยายฟังก์ชันในอนุกรมกำลัง:

เพื่อคำนวณค่าโดยประมาณของฟังก์ชัน ณ จุดที่กำหนด เอ็กซ์ซึ่งอยู่ในขอบเขตของการบรรจบกันของซีรีส์ที่ระบุ ซีรีส์แรกจะเหลืออยู่ในส่วนขยาย nสมาชิก ( n– จำนวนจำกัด) และเงื่อนไขที่เหลือให้ละทิ้ง:

ในการประมาณค่าความผิดพลาดของค่าโดยประมาณที่ได้รับ จำเป็นต้องประมาณค่าเศษที่เหลือทิ้ง rn (x) . เมื่อต้องการทำเช่นนี้ ใช้เทคนิคต่อไปนี้:

• หากอนุกรมผลลัพธ์สลับกัน จะใช้คุณสมบัติต่อไปนี้: สำหรับอนุกรมสลับที่เป็นไปตามเงื่อนไขของไลบ์นิซ ส่วนที่เหลือของอนุกรมในค่าสัมบูรณ์จะต้องไม่เกินเทอมแรกที่ถูกละทิ้ง.
• ถ้าอนุกรมที่กำหนดมีเครื่องหมายคงที่ อนุกรมที่ประกอบด้วยคำศัพท์ที่ถูกละทิ้งจะถูกเปรียบเทียบกับความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด
• ในกรณีทั่วไป หากต้องการประมาณค่าส่วนที่เหลือของอนุกรม Taylor คุณสามารถใช้สูตรลากรองจ์ได้: x ).

ตัวอย่างหมายเลข 1 คำนวณ ln(3) ให้ใกล้ที่สุด 0.01
สารละลาย- ลองใช้ส่วนขยายโดยที่ x=1/2 (ดูตัวอย่างที่ 5 ในหัวข้อที่แล้ว):

เรามาตรวจสอบว่าเราสามารถทิ้งส่วนที่เหลือหลังจากสามเทอมแรกของการขยายตัวได้หรือไม่ โดยเราจะประเมินมันโดยใช้ผลรวมของความก้าวหน้าทางเรขาคณิตที่ลดลงอย่างไม่สิ้นสุด:

เราก็ทิ้งเศษนี้แล้วได้

ตัวอย่างหมายเลข 2 คำนวณหาค่าที่ใกล้ที่สุด 0.0001
สารละลาย- ลองใช้อนุกรมทวินามกัน. เนื่องจาก 5 3 เป็นกำลังสามของจำนวนเต็มที่ใกล้กับ 130 มากที่สุด จึงแนะนำให้แสดงตัวเลข 130 เป็น 130 = 5 3 +5



เนื่องจากเทอมที่สี่ของอนุกรมการสลับผลลัพธ์ที่เป็นไปตามเกณฑ์ของไลบ์นิซนั้นน้อยกว่าความแม่นยำที่ต้องการ:
ดังนั้นจึงสามารถยกเลิกและข้อกำหนดต่อไปนี้ได้
อินทิกรัลที่แน่นอนหรือไม่เหมาะสมที่จำเป็นในทางปฏิบัติจำนวนมากไม่สามารถคำนวณได้โดยใช้สูตรของนิวตัน-ไลบ์นิซ เนื่องจากการประยุกต์ของสูตรนี้เกี่ยวข้องกับการหาแอนติเดริเวทีฟ ซึ่งมักไม่มีนิพจน์ในฟังก์ชันพื้นฐาน นอกจากนี้ยังเกิดขึ้นอีกด้วยว่าการค้นหาแอนติเดริเวทีฟนั้นเป็นไปได้ แต่ต้องใช้แรงงานมากโดยไม่จำเป็น อย่างไรก็ตาม หากฟังก์ชันจำนวนเต็มถูกขยายเป็นอนุกรมกำลัง และขีดจำกัดของการรวมอยู่ในช่วงของการลู่เข้าของอนุกรมนี้ การคำนวณค่าอินทิกรัลโดยประมาณด้วยความแม่นยำที่กำหนดไว้ล่วงหน้าจึงเป็นไปได้

ตัวอย่างหมายเลข 3 คำนวณอินทิกรัล ∫ 0 1 4 sin (x) x ภายใน 10 -5
สารละลาย- อินทิกรัลไม่ จำกัด ที่สอดคล้องกันไม่สามารถแสดงในฟังก์ชันพื้นฐานได้เช่น แสดงถึง “อินทิกรัลไม่ถาวร” ไม่สามารถใช้สูตรของนิวตัน-ไลบ์นิซได้ที่นี่ ลองคำนวณอินทิกรัลโดยประมาณกัน
แบ่งคำศัพท์ตามลำดับสำหรับความบาป xบน x, เราได้รับ:

การรวมคำศัพท์ของอนุกรมนี้ทีละเทอม (เป็นไปได้ เนื่องจากขีดจำกัดของการรวมเป็นช่วงของการบรรจบกันของอนุกรมนี้) เราได้รับ:

เนื่องจากอนุกรมผลลัพธ์เป็นไปตามเงื่อนไขของไลบ์นิซ และเพียงพอที่จะนำผลรวมของสองเทอมแรกเพื่อให้ได้ค่าที่ต้องการด้วยความแม่นยำที่กำหนด
ดังนั้นเราจึงพบว่า
.

ตัวอย่างหมายเลข 4 คำนวณอินทิกรัล ∫ 0 1 4 e x 2 ด้วยความแม่นยำ 0.001
สารละลาย.
- ลองตรวจสอบว่าเราสามารถทิ้งส่วนที่เหลือหลังจากเทอมที่สองของอนุกรมผลลัพธ์ได้หรือไม่
0.0001<0.001. Следовательно, .