บทเรียน "ฟังก์ชันตรีโกณมิติของการโต้แย้งเชิงมุม" ฟังก์ชันตรีโกณมิติของอาร์กิวเมนต์เชิงตัวเลขและเชิงมุม การวัดองศาของมุม

บทเรียนและการนำเสนอในหัวข้อ: "ฟังก์ชันตรีโกณมิติของอาร์กิวเมนต์เชิงมุม การวัดองศาของมุมและเรเดียน"

วัสดุเพิ่มเติม
เรียนผู้ใช้ อย่าลืมแสดงความคิดเห็น บทวิจารณ์ และความปรารถนาของคุณ วัสดุทั้งหมดได้รับการตรวจสอบโดยโปรแกรมป้องกันไวรัส

คู่มือและตัวจำลองในร้านค้าออนไลน์ Integral สำหรับเกรด 10 จาก 1C
เราแก้ปัญหาในเรขาคณิต งานอาคารแบบโต้ตอบ
เราแก้ปัญหาในเรขาคณิต งานแบบโต้ตอบสำหรับการสร้างในอวกาศ

เราจะศึกษาอะไร:
1. มาจำเรขาคณิตกัน
2. คำจำกัดความของอาร์กิวเมนต์เชิงมุม
3. การวัดองศาของมุม
4. การวัดมุมเรเดียน
5. เรเดียนคืออะไร?
6. ตัวอย่างและงานสำหรับโซลูชันอิสระ

การทำซ้ำของเรขาคณิต

พวกเราในหน้าที่ของเรา:

y= บาป(t), y= cos(t), y= tg(t), y= ctg(t)

ตัวแปร t ไม่เพียงแต่รับค่าตัวเลขเท่านั้น นั่นคือเป็นอาร์กิวเมนต์ตัวเลข แต่ยังถือได้ว่าเป็นการวัดมุม - อาร์กิวเมนต์เชิงมุมอีกด้วย

มาจำเรขาคณิตกันเถอะ!
เรานิยามไซน์, โคไซน์, แทนเจนต์, โคแทนเจนต์ตรงนั้นได้อย่างไร?

ไซน์ของมุม - อัตราส่วนของด้านตรงข้ามกับด้านตรงข้ามมุมฉาก

โคไซน์ของมุม - อัตราส่วนของขาที่อยู่ติดกันต่อด้านตรงข้ามมุมฉาก

แทนเจนต์ของมุมคืออัตราส่วนของด้านตรงข้ามกับด้านประชิด

โคแทนเจนต์ของมุมคืออัตราส่วนของด้านประชิดต่อด้านตรงข้าม

คำจำกัดความของฟังก์ชันตรีโกณมิติของการโต้แย้งมุม

ลองนิยามฟังก์ชันตรีโกณมิติเป็นฟังก์ชันของอาร์กิวเมนต์เชิงมุมบนวงกลมตัวเลข:
เมื่อใช้วงกลมจำนวนและระบบพิกัด เราสามารถค้นหาไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์ของมุมได้อย่างง่ายดาย:

ลองวางจุดยอดของมุม α ของเราไว้ที่ศูนย์กลางของวงกลม นั่นคือ ไปที่ศูนย์กลางของแกนพิกัดและวางด้านใดด้านหนึ่งให้ตรงกับทิศทางบวกของแกนแอบซิสซา (OA)
จากนั้นด้านที่สองตัดวงกลมตัวเลขที่จุด M

บวชจุด M: ไซน์ของมุม α
แอบซิสซาจุด M: โคไซน์ของมุม α

โปรดทราบว่าความยาวส่วนโค้ง AM เป็นส่วนเดียวกับวงกลมหนึ่งหน่วยกับมุม α จาก 360 องศา: โดยที่ t คือความยาวของส่วนโค้ง AM

องศาการวัดมุม

1) เพื่อนๆ เรามีสูตรสำหรับกำหนดองศาของมุมผ่านความยาวส่วนโค้งของวงกลมตัวเลข มาดูกันดีกว่า:

จากนั้นเราเขียนฟังก์ชันตรีโกณมิติในรูปแบบ:

ตัวอย่างเช่น:

การวัดมุมเรเดียน

เมื่อคำนวณค่าองศาหรือเรเดียนของมุม จำไว้! -
ตัวอย่างเช่น:

อนึ่ง! การกำหนด rad. คุณสามารถลดมันลงได้!

เรเดียนคืออะไร?

เพื่อน ๆ ที่รัก เรากำลังเผชิญกับแนวคิดใหม่ - เรเดียน- แล้วมันคืออะไร?

มีหน่วยวัดความยาว เวลา น้ำหนักได้หลากหลาย เช่น เมตร กิโลเมตร วินาที ชั่วโมง กรัม กิโลกรัม และอื่นๆ เรเดียนก็เป็นหนึ่งในหน่วยวัดมุม ควรพิจารณามุมที่อยู่ตรงกลางนั่นคือมุมที่อยู่ตรงกลางวงกลมตัวเลข
มุม 1 องศา คือ มุมศูนย์กลางที่ต่อด้วยส่วนโค้งเท่ากับ 1/360 ของเส้นรอบวง

มุม 1 เรเดียน คือ มุมที่จุดศูนย์กลางต่อด้วยส่วนโค้งเท่ากับ 1 ในวงกลมหนึ่งหน่วย และในวงกลมใดๆ ก็ได้ด้วยส่วนโค้งเท่ากับรัศมีของวงกลม

ตัวอย่าง:

ตัวอย่างการแปลงจากการวัดระดับของมุมเป็นการวัดเรเดียน และในทางกลับกัน

ปัญหาที่ต้องแก้ไขอย่างอิสระ

1. ค้นหาการวัดมุมเรเดียน:
ก) 55° ข) 450° ค) 15° ง) 302°

2. ค้นหา:
ก) บาป(150°) b) cos(45°) c) tg(120°)

3. ค้นหาการวัดระดับของมุม:

ฟังก์ชันตรีโกณมิติของอาร์กิวเมนต์ตัวเลขเราแยกมันออก เราหาจุด A บนวงกลมแล้วมองหาไซน์และโคไซน์ของมุมผลลัพธ์ β

เรากำหนดจุดเป็น A แต่ในพีชคณิตมักถูกกำหนดเป็น t และมีการกำหนดสูตร/ฟังก์ชันทั้งหมดให้กับจุดนั้น เราจะไม่เบี่ยงเบนไปจากศีลด้วย เหล่านั้น. t - นี่จะเป็นจำนวนที่แน่นอน ฟังก์ชันตัวเลข(เช่น บาป t)

เป็นตรรกะที่เนื่องจากเรามีวงกลมที่มีรัศมีหนึ่งแล้ว

ฟังก์ชันตรีโกณมิติของการโต้แย้งมุมนอกจากนี้เรายังวิเคราะห์ได้สำเร็จ - ตามหลักการเราจะเขียนสำหรับฟังก์ชันดังกล่าว: sin α° ซึ่งหมายถึง α° มุมใดก็ได้ตามจำนวนองศาที่เราต้องการ

รังสีของมุมนี้จะให้จุดที่สองบนวงกลมแก่เรา (OA - จุด A) และจุด C และ B ที่สอดคล้องกันสำหรับฟังก์ชันอาร์กิวเมนต์ตัวเลขหากเราต้องการ: บาป t = บาป α°

เส้นไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์

อย่าลืมสิ่งนั้น แกน Y คือเส้นไซน์, แกน X คือเส้นโคไซน์- คะแนนที่ได้จากวงกลมจะถูกทำเครื่องหมายไว้บนแกนเหล่านี้

ก เส้นแทนเจนต์และโคแทนเจนต์ขนานกันและผ่านจุด (1; 0) และ (0; 1)ตามลำดับ

บทเรียนวิดีโอ "ฟังก์ชันตรีโกณมิติของการโต้แย้งเชิงมุม" มีเนื้อหาภาพสำหรับการดำเนินการบทเรียนคณิตศาสตร์ในหัวข้อที่เกี่ยวข้อง วิดีโอนี้ได้รับการออกแบบเพื่อให้นำเสนอเนื้อหาที่กำลังศึกษาได้อย่างสะดวกที่สุดเพื่อให้นักเรียนเข้าใจ จดจำง่าย และเผยให้เห็นความเชื่อมโยงระหว่างข้อมูลที่มีอยู่เกี่ยวกับฟังก์ชันตรีโกณมิติจากส่วนการศึกษารูปสามเหลี่ยมและคำจำกัดความโดยใช้หน่วย วงกลม. บทเรียนนี้สามารถกลายเป็นส่วนอิสระของบทเรียนได้ เนื่องจากครอบคลุมหัวข้อนี้อย่างครบถ้วน พร้อมด้วยข้อคิดเห็นที่สำคัญระหว่างการออกเสียง

เพื่อแสดงให้เห็นความสัมพันธ์ระหว่างคำจำกัดความต่างๆ ของฟังก์ชันตรีโกณมิติได้อย่างชัดเจน จึงมีการใช้เอฟเฟ็กต์แอนิเมชัน การเน้นข้อความด้วยแบบอักษรสี โครงสร้างที่ชัดเจน เข้าใจง่าย และการเพิ่มความคิดเห็นจะช่วยให้คุณเชี่ยวชาญและจดจำเนื้อหาได้อย่างรวดเร็ว และบรรลุเป้าหมายของบทเรียนได้อย่างรวดเร็ว การเชื่อมโยงระหว่างคำจำกัดความของฟังก์ชันตรีโกณมิติแสดงให้เห็นอย่างชัดเจนผ่านเอฟเฟ็กต์แอนิเมชันและการเน้นสี ซึ่งส่งเสริมความเข้าใจและการเก็บรักษาวัสดุ คู่มือนี้มีวัตถุประสงค์เพื่อเพิ่มประสิทธิผลของการฝึกอบรม

บทเรียนเริ่มต้นด้วยการแนะนำหัวข้อ จากนั้นจะนึกถึงคำจำกัดความของไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ของมุมแหลมของรูปสามเหลี่ยมมุมฉาก คำจำกัดความที่ไฮไลต์ในกรอบเตือนเราว่าไซน์และโคไซน์ก่อตัวขึ้นเมื่ออัตราส่วนของขาต่อด้านตรงข้ามมุมฉาก แทนเจนต์และโคแทนเจนต์เกิดจากอัตราส่วนของขา นักเรียนยังนึกถึงสื่อการเรียนรู้เมื่อเร็วๆ นี้ว่าเมื่อพิจารณาจุดบนวงกลมหน่วย สมการของจุดคือโคไซน์ และพิกัดคือไซน์ของตัวเลขที่ตรงกับจุดนั้น ความเชื่อมโยงระหว่างแนวคิดเหล่านี้แสดงให้เห็นโดยใช้การก่อสร้าง หน้าจอจะแสดงวงกลมหนึ่งหน่วยซึ่งวางอยู่ตรงกลางเพื่อให้ตรงกับจุดกำเนิด จากจุดกำเนิดของพิกัด รังสีถูกสร้างขึ้นเพื่อสร้างมุม α โดยมีแกนกึ่งแกนแอบซิสซาที่เป็นบวก รังสีนี้ตัดกับวงกลมหนึ่งหน่วยที่จุด O จากจุดนั้น เส้นตั้งฉากลงมาที่แอบซิสซาและกำหนดแกน แสดงให้เห็นว่าพิกัดของจุดนี้เป็นตัวกำหนดโคไซน์และไซน์ของมุม α สังเกตว่าความยาวของส่วนโค้ง AO จากจุดตัดของวงกลมหนึ่งหน่วยที่มีทิศทางบวกของแกนแอบซิสซาถึงจุด O ถือเป็นส่วนเดียวกันของส่วนโค้งทั้งหมดเท่ากับมุม α จาก 360° วิธีนี้ช่วยให้คุณสร้างสัดส่วน α/360=t/2π ซึ่งจะแสดงทันทีและไฮไลต์ด้วยสีแดงเพื่อจดจำ จากสัดส่วนนี้ จะได้ค่า t=πα/180° เมื่อคำนึงถึงสิ่งนี้ ความสัมพันธ์ระหว่างคำจำกัดความของไซน์และโคไซน์จึงถูกกำหนด: sinα°= sint= sinπα/180, cosα°=cost=cosπα/180 ตัวอย่างเช่น ให้การหา sin60° เมื่อแทนค่าองศาของมุมลงในสูตร เราจะได้ sin π·60°/180° เมื่อลดเศษส่วนลง 60 เราจะได้ sin π/3 ซึ่งเท่ากับ √3/2 มีข้อสังเกตว่าถ้า 60° เป็นหน่วยวัดองศาของมุม แล้ว π/3 จะเรียกว่าหน่วยวัดเรเดียนของมุม มีสองสัญลักษณ์ที่เป็นไปได้สำหรับอัตราส่วนของการวัดระดับของมุมต่อการวัดเรเดียน: 60°=π/3 และ 60°=π/3 rad

แนวคิดของมุมหนึ่งองศาถูกกำหนดให้เป็นมุมที่อยู่ตรงกลางซึ่งต่อด้วยส่วนโค้งซึ่งมีความยาว 1/360 แสดงถึงส่วนหนึ่งของเส้นรอบวง คำจำกัดความต่อไปนี้เผยให้เห็นแนวคิดของมุมหนึ่งเรเดียน ซึ่งเป็นมุมที่ศูนย์กลางขึ้นอยู่กับส่วนโค้งที่มีความยาวหนึ่งหรือเท่ากับรัศมีของวงกลม คำจำกัดความถูกทำเครื่องหมายว่าสำคัญและเน้นให้จดจำ

หากต้องการแปลงการวัดมุมหนึ่งองศาเป็นการวัดเรเดียนและในทางกลับกัน ให้ใช้สูตร α°=πα/180 rad สูตรนี้ไฮไลท์อยู่ในกรอบบนหน้าจอ จากสูตรนี้ จะได้ว่า 1° = π/180 rad ในกรณีนี้ หนึ่งเรเดียนจะสัมพันธ์กับมุม 180°/πθ57.3° มีข้อสังเกตว่าเมื่อค้นหาค่าของฟังก์ชันตรีโกณมิติของตัวแปรอิสระ t ก็สามารถพิจารณาได้ทั้งอาร์กิวเมนต์เชิงตัวเลขและเชิงมุม

ต่อไปนี้เป็นตัวอย่างการใช้ความรู้ที่ได้รับในการแก้ปัญหาทางคณิตศาสตร์ ในตัวอย่างที่ 1 คุณต้องแปลงค่าจากองศาเป็นเรเดียน 135° และ 905° ทางด้านขวาของหน้าจอจะมีสูตรแสดงความสัมพันธ์ระหว่างองศากับเรเดียน หลังจากแทนค่าลงในสูตรแล้ว เราจะได้ (π/180)·135 หลังจากลดเศษส่วนนี้ลง 45 เราจะได้ค่า 135° = 3π/4 ในการแปลงมุม 905° เป็นหน่วยวัดเรเดียน จะใช้สูตรเดียวกัน หลังจากแทนค่าลงไปแล้ว จะได้ว่า (π/180)·905=181π/36 rad

ในตัวอย่างที่สอง ปัญหาผกผันได้รับการแก้ไขแล้ว โดยจะพบระดับของมุมที่แสดงเป็นเรเดียน π/12, -21π/20, 2.4π ที่ด้านขวาของหน้าจอ เราจะนึกถึงสูตรที่ศึกษาสำหรับการเชื่อมต่อระหว่างการวัดองศากับเรเดียนของมุม 1 rad = 180°/π แต่ละตัวอย่างได้รับการแก้ไขโดยการแทนที่หน่วยวัดเรเดียนลงในสูตร เมื่อแทน π/12 เราจะได้ (180°/π)·(π/12)=15° ค่าของมุมที่เหลือจะพบในทำนองเดียวกัน -21π/20=-189° และ 2.4π=432°

แนะนำให้ใช้วิดีโอบทเรียน "ฟังก์ชันตรีโกณมิติของการโต้แย้งเชิงมุม" เพื่อใช้ในบทเรียนคณิตศาสตร์แบบดั้งเดิมเพื่อเพิ่มประสิทธิภาพการเรียนรู้ เนื้อหานี้จะช่วยให้มั่นใจได้ถึงการมองเห็นการเรียนรู้ระหว่างการเรียนทางไกลในหัวข้อนี้ คำอธิบายโดยละเอียดและเข้าใจง่ายของหัวข้อและวิธีการแก้ไขปัญหาสามารถช่วยให้นักเรียนเชี่ยวชาญเนื้อหาได้อย่างอิสระ

การถอดรหัสข้อความ:

"ฟังก์ชันตรีโกณมิติของอาร์กิวเมนต์เชิงมุม"

จากเรขาคณิตเรารู้อยู่แล้วว่าไซน์ (โคไซน์) ของมุมแหลมของสามเหลี่ยมมุมฉากคืออัตราส่วนของขาต่อด้านตรงข้ามมุมฉาก และแทนเจนต์ (โคแทนเจนต์) คืออัตราส่วนของขา ในพีชคณิต เราเรียกจุดแอบซิสซาของจุดบนวงกลมหนึ่งหน่วยว่าโคไซน์ และพิกัดของจุดนี้ว่าไซน์ ตรวจสอบให้แน่ใจว่าทั้งหมดนี้เชื่อมโยงกันอย่างใกล้ชิด

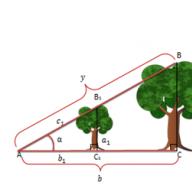
ลองวางมุมด้วยการวัดระดับ α° (องศาอัลฟา) ดังแสดงในรูปที่ 1: จุดยอดของมุมเข้ากันได้กับจุดศูนย์กลางของวงกลมหน่วย (ที่มีต้นกำเนิดของระบบพิกัด) และด้านหนึ่งของมุม เข้ากันได้กับรังสีบวกของแกนแอบซิสซา ด้านที่สองของมุมตัดกับวงกลมที่จุด O พิกัดของจุด O คือไซน์ของมุมอัลฟา และค่าแอบซิสซาของจุดนี้คือโคไซน์ของอัลฟ่า

โปรดทราบว่าส่วนโค้ง AO เป็นส่วนเดียวกันกับความยาวของวงกลมหนึ่งหน่วย เนื่องจากมุมอัลฟามาจากมุมสามร้อยหกสิบองศา ให้เราแทนความยาวของส่วนโค้ง AO ด้วย t(te) จากนั้นเราจะเขียนสัดส่วน =

(อัลฟาคือการเชื่อถือหกสิบเช่นเดียวกับ te เท่ากับสองไพ) จากตรงนี้เราจะพบ te: t = = (te เท่ากับ pi alpha หารด้วยหนึ่งร้อยแปดสิบ)

ดังนั้น หากต้องการหาไซน์หรือโคไซน์ของมุม อัลฟ่า องศา คุณสามารถใช้สูตรได้:

sin α° = sint = sin (องศาไซน์อัลฟาเท่ากับไซน์ te และเท่ากับไซน์ของไพอัลฟาบางส่วนถึงหนึ่งร้อยแปดสิบ)

cosα° = cost = cos (โคไซน์ขององศาอัลฟาเท่ากับโคไซน์ของ te และเท่ากับโคไซน์ของพายอัลฟาบางส่วนถึงหนึ่งร้อยแปดสิบ)

ตัวอย่างเช่น sin 60° = sin = sin = (ไซน์ของหกสิบองศาเท่ากับไซน์ของ pi คูณสาม ตามตารางค่าพื้นฐานของไซน์จะเท่ากับรากของสามคูณสอง) .

เชื่อกันว่า 60° เป็นหน่วยวัดระดับของมุม และ (pi คูณสาม) เป็นหน่วยวัดเรเดียนของมุมเดียวกัน นั่นคือ 60° = ยินดี(หกสิบองศาเท่ากับพายคูณสามเรเดียน) เพื่อความกระชับเราตกลงกันในเรื่องการกำหนด ยินดีละเว้น นั่นคือ รายการต่อไปนี้เป็นที่ยอมรับ: 60°= (แสดงตัวย่อ เรเดียน หน่วยวัด = rad)

มุมหนึ่งองศาคือมุมที่ศูนย์กลางซึ่งรองรับส่วนโค้งที่เป็นส่วนหนึ่งของส่วนโค้ง (หนึ่งสามร้อยหกสิบ) มุมของหนึ่งเรเดียนคือมุมที่อยู่ตรงกลางซึ่งวางอยู่บนส่วนโค้งที่มีความยาวหนึ่ง นั่นคือ ส่วนโค้งที่มีความยาวเท่ากับรัศมีของวงกลม (เราพิจารณามุมที่ศูนย์กลางของวงกลมหนึ่งหน่วยเพื่อแสดงมุมในหน่วย pi เรเดียน บนวงกลม)

ให้เราจำสูตรสำคัญในการแปลงองศาเป็นเรเดียน:

α° = ยินดี- (อัลฟาเท่ากับไพอัลฟาหารด้วยหนึ่งร้อยแปดสิบเรเดียน) โดยเฉพาะ 1° = ยินดี(หนึ่งองศาเท่ากับพายหารด้วยหนึ่งร้อยแปดสิบเรเดียน)

จากนี้ เราจะพบว่าหนึ่งเรเดียนเท่ากับอัตราส่วนหนึ่งร้อยแปดสิบองศาต่อพาย และมีค่าประมาณเท่ากับห้าสิบเจ็ดจุดสามองศา: 1 ยินดี= อยู่ที่ 57.3°

จากที่กล่าวมาข้างต้น: เมื่อเราพูดถึงฟังก์ชันตรีโกณมิติใดๆ เช่น ฟังก์ชัน s = sint (es เท่ากับไซน์ te) ตัวแปรอิสระ t(te) ถือได้ว่าเป็นทั้งอาร์กิวเมนต์เชิงตัวเลขและอาร์กิวเมนต์เชิงมุม

ลองดูตัวอย่าง

ตัวอย่างที่ 1 แปลงจากองศาเป็นเรเดียน: ก) 135°; ข) 905°

สารละลาย. ลองใช้สูตรแปลงองศาเป็นเรเดียน:

ก) 135° = 1° ∙ 135 = ยินดี ∙ 135 = ยินดี

(หนึ่งร้อยสามสิบห้าองศาเท่ากับพายคูณหนึ่งร้อยแปดสิบเรเดียนคูณด้วยหนึ่งร้อยสามสิบห้า และหลังการลดลงเท่ากับสามไพคูณสี่เรเดียน)

b) ในทำนองเดียวกันเราได้รับการใช้สูตรสำหรับการแปลงหน่วยวัดระดับเป็นหน่วยวัดเรเดียน

905° = ยินดี ∙ 905 = ยินดี.

(เก้าร้อยห้าองศาเท่ากับหนึ่งร้อยแปดสิบเอ็ดไพคูณสามสิบหกเรเดียน)

ตัวอย่าง 2. แสดงเป็นองศา: a) ; ข) - ; ค) 2.4π

(พายส่วนสิบสอง; ลบยี่สิบเอ็ดพายส่วนยี่สิบ; สองจุดสี่พาย)

สารละลาย. ก) ลองเขียนค่าพายเป็น 12 องศา โดยใช้สูตรแปลงค่าเรเดียนของมุมเป็นองศาใน 1 ยินดี= เราเข้าใจแล้ว

ยินดี = 1 ยินดี∙ = ∙ = 15° (พายคูณสิบสองเรเดียนจะเท่ากับผลคูณของหนึ่งเรเดียนและพายคูณสิบสอง เมื่อแทนหนึ่งร้อยแปดสิบด้วยพายแทนที่จะเป็นหนึ่งเรเดียนแล้วลด เราก็จะได้สิบห้าองศา)

คล้ายกับ b) - = 1 ยินดี∙ (-) = ∙ (-)= - 189° (ลบยี่สิบเอ็ดไพคูณยี่สิบเท่ากับลบหนึ่งร้อยแปดสิบเก้าองศา)

ค) 2.4π = 1 ยินดี∙ 2.4π = ∙ 2.4π = 432° (สองจุดสี่พายเท่ากับสี่ร้อยสามสิบสององศา)

ไม่ว่าจะใช้จำนวนจริง t ใดก็ตาม มันสามารถเชื่อมโยงกับจำนวน sin t ที่กำหนดโดยเฉพาะได้ จริงอยู่ กฎการจับคู่ค่อนข้างซับซ้อน ดังที่เราเห็นข้างต้น จะเป็นดังนี้

ในการค้นหาค่าของ sin t โดยใช้ตัวเลข t คุณต้องมี:

1) วางตำแหน่งวงกลมตัวเลขในระนาบพิกัดเพื่อให้ศูนย์กลางของวงกลมตรงกับที่มาของพิกัด และจุดเริ่มต้น A ของวงกลมตกอยู่ที่จุด (1; 0)

2) ค้นหาจุดบนวงกลมที่ตรงกับตัวเลข t;

3) ค้นหาพิกัดของจุดนี้

ลำดับนี้เป็นบาป t

อันที่จริง เรากำลังพูดถึงฟังก์ชัน u = sin t โดยที่ t คือจำนวนจริงใดๆ

ฟังก์ชันทั้งหมดนี้เรียกว่า ฟังก์ชันตรีโกณมิติของอาร์กิวเมนต์ตัวเลข t

มีความสัมพันธ์หลายอย่างที่เชื่อมโยงค่าของฟังก์ชันตรีโกณมิติต่างๆ เราได้รับความสัมพันธ์เหล่านี้บางส่วนแล้ว:

บาป 2 t+cos 2 t = 1

จากสองสูตรสุดท้าย การหาความสัมพันธ์ระหว่าง tg t และ ctg t เป็นเรื่องง่าย:

สูตรทั้งหมดเหล่านี้ใช้ในกรณีที่เมื่อทราบค่าของฟังก์ชันตรีโกณมิติจึงจำเป็นต้องคำนวณค่าของฟังก์ชันตรีโกณมิติอื่น ๆ

จริงๆ แล้วคำว่า "ไซน์", "โคไซน์", "แทนเจนต์" และ "โคแทนเจนต์" เป็นคำคุ้นเคย อย่างไรก็ตาม ยังคงใช้ในการตีความที่แตกต่างกันเล็กน้อย: ในเรขาคณิตและฟิสิกส์ พวกเขาถือว่าไซน์ โคไซน์ แทนเจนต์ และโคแทนเจนต์ ที่ศีรษะ(แต่ไม่

ตัวเลขเหมือนในย่อหน้าก่อนๆ)

จากเรขาคณิต เป็นที่ทราบกันว่าไซน์ (โคไซน์) ของมุมแหลมคืออัตราส่วนของขาของสามเหลี่ยมมุมฉากต่อด้านตรงข้ามมุมฉาก และแทนเจนต์ (โคแทนเจนต์) ของมุมคืออัตราส่วนของขาของสามเหลี่ยมมุมฉาก แนวทางที่แตกต่างสำหรับแนวคิดของไซน์ โคไซน์ แทนเจนต์และโคแทนเจนต์ได้รับการพัฒนาในย่อหน้าก่อนหน้านี้ ที่จริงแล้วแนวทางเหล่านี้มีความสัมพันธ์กัน

ลองหามุมที่มีหน่วยวัดองศา b o แล้ววางไว้ในแบบจำลอง “วงกลมตัวเลขในระบบพิกัดสี่เหลี่ยม” ดังแสดงในรูป 14

ยอดของมุมเข้ากันได้กับจุดศูนย์กลาง

วงกลม (ที่มีต้นกำเนิดของระบบพิกัด)

และมุมด้านหนึ่งก็เข้ากันได้

รังสีบวกของแกน x หยุดเต็ม

จุดตัดของด้านที่สองของมุมด้วย

แทนวงกลมด้วยตัวอักษร M. Ordina-

รูปที่ 14 b o และ abscissa ของจุดนี้คือโคไซน์ของมุม b o

ในการค้นหาไซน์หรือโคไซน์ของมุม ไม่จำเป็นต้องสร้างโครงสร้างที่ซับซ้อนมากทุกครั้งเลย

ก็เพียงพอแล้วที่จะสังเกตว่าส่วนโค้ง AM ประกอบขึ้นเป็นส่วนหนึ่งของความยาวของวงกลมตัวเลขเหมือนกับที่มุม b o สร้างจากมุม 360° หากความยาวของส่วนโค้ง AM แสดงด้วยตัวอักษร t เราจะได้:

ดังนั้น,

ตัวอย่างเช่น,

เชื่อกันว่า 30° เป็นหน่วยวัดองศาของมุม และหน่วยวัดเรเดียนของมุมเดียวกัน: 30° = rad ทั้งหมด:

โดยเฉพาะอย่างยิ่งฉันดีใจที่เราได้มันมาจากไหน

แล้ว 1 เรเดียนคืออะไร? ความยาวของเซ็กเมนต์มีหน่วยวัดต่างๆ เช่น เซนติเมตร เมตร หลา ฯลฯ นอกจากนี้ยังมีมาตรการต่างๆ เพื่อระบุขนาดของมุม เราพิจารณามุมที่ศูนย์กลางของวงกลมหน่วย มุม 1° คือมุมศูนย์กลางที่ต่อด้วยส่วนโค้งที่เป็นส่วนหนึ่งของวงกลม มุม 1 เรเดียน คือ มุมที่จุดศูนย์กลางต่อด้วยส่วนโค้งยาว 1 กล่าวคือ บนส่วนโค้งที่มีความยาวเท่ากับรัศมีของวงกลม จากสูตร เราพบว่า 1 ราด = 57.3°

เมื่อพิจารณาฟังก์ชัน u = sin t (หรือฟังก์ชันตรีโกณมิติอื่น ๆ ) เราสามารถพิจารณาตัวแปรอิสระ t ให้เป็นอาร์กิวเมนต์เชิงตัวเลขได้ ดังเช่นในกรณีในย่อหน้าก่อนหน้า แต่เรายังพิจารณาตัวแปรนี้เพื่อใช้วัดได้ด้วย มุมเช่น อาร์กิวเมนต์มุม ดังนั้น เมื่อพูดถึงฟังก์ชันตรีโกณมิติ ในแง่หนึ่ง การพิจารณาว่าฟังก์ชันนี้เป็นฟังก์ชันของอาร์กิวเมนต์เชิงตัวเลขหรือเชิงมุมก็ไม่ต่างกัน