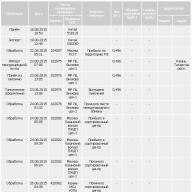
Rotirea unui corp rigid în jurul unei axe fixe se numește o astfel de mișcare în care două puncte ale corpului rămân nemișcate pe toată durata mișcării. În acest caz, toate punctele corpului, situate pe o linie dreaptă care trece prin punctele sale fixe, rămân și ele nemișcate. Această linie se numește axa de rotație a corpului .
Punctele A și B să fie fixe. Direcționați axa de-a lungul axei de rotație. Prin axa de rotație desenăm un plan fix și unul mobil, fixat pe un corp rotativ (at).
Poziția planului și a corpului însuși este determinată de unghiul diedric dintre planuri și. Să-l desemnăm. Unghiul se numește unghiul de rotație al corpului .
Poziția corpului față de cadrul de referință selectat este determinată în mod unic în orice moment de timp dacă este dată ecuația, unde este orice funcție de timp diferențiabilă de două ori. Această ecuație se numește ecuația de rotație a unui corp rigid în jurul unei axe fixe .
Un corp care se rotește în jurul unei axe fixe are un grad de libertate, deoarece poziția sa este determinată prin specificarea unui singur parametru - unghiul.
Un unghi este considerat pozitiv dacă este reprezentat în sens invers acelor de ceasornic și negativ în direcția opusă. Traiectoriile punctelor unui corp atunci când acesta se rotește în jurul unei axe fixe sunt cercuri situate în planuri perpendiculare pe axa de rotație.
Pentru a caracteriza mișcarea de rotație a unui corp rigid în jurul unei axe fixe, introducem conceptele de viteză unghiulară și accelerație unghiulară.
Viteza unghiulară algebrică corpul în orice moment în timp se numește prima derivată temporală a unghiului de rotație în acel moment, adică.
Viteza unghiulară este o valoare pozitivă când corpul se rotește în sens invers acelor de ceasornic, deoarece unghiul de rotație crește cu timpul, și negativă când corpul se rotește în sensul acelor de ceasornic, deoarece unghiul de rotație scade.
Dimensiunea vitezei unghiulare prin definiție:
În inginerie, viteza unghiulară este viteza de rotație exprimată în rotații pe minut. Într-un minut, corpul se va întoarce printr-un unghi, unde n este numărul de rotații pe minut. Împărțind acest unghi la numărul de secunde dintr-un minut, obținem
Accelerația unghiulară algebrică a unui corp se numește prima derivată temporală a vitezei unghiulare, adică derivata a doua a unghiului de rotație, adică.
Dimensiunea accelerației unghiulare prin definiție:
Să introducem conceptele de vectori de viteză unghiulară și accelerație unghiulară a unui corp.
Și, unde este vectorul unitar al axei de rotație. Vectori și pot fi desenați în orice punct al axei de rotație, sunt vectori de alunecare.
Viteza unghiulară algebrică este proiecția vectorului viteză unghiulară pe axa de rotație. Accelerația unghiulară algebrică este proiecția vectorului viteză unghiulară pe axa de rotație.
Dacă la, atunci viteza unghiulară algebrică crește cu timpul și, prin urmare, corpul se rotește cu o viteză accelerată în momentul în cauză în direcția pozitivă. Direcțiile vectorilor și coincid, ambele sunt îndreptate spre partea pozitivă a axei de rotație.
La și, corpul se rotește cu accelerație în direcția negativă. Direcțiile vectorilor și coincid, ambele sunt îndreptate spre partea negativă a axei de rotație.
Mișcarea de rotație a unui corp rigid. Rotația este mișcarea unui corp rigid în care toate punctele sale situate pe o anumită linie dreaptă, numită axa de rotație, rămân nemișcate.
În timpul mișcării de rotație, toate celelalte puncte ale corpului se mișcă în planuri perpendiculare pe axa de rotație și descriu cercuri, ale căror centre se află pe această variolă.
Pentru a determina poziția corpului în rotație, desenăm două semiplane prin axa z: semiplanul I - staționar și semiplanul II - asociat cu un corp rigid și care se rotește cu acesta (Fig. 2.4). Atunci poziția corpului în orice moment în timp va fi determinată în mod unic de unghi jîntre aceste semiplane, luate cu semnul corespunzător, care se numește unghiul de rotație al corpului.
Când corpul se rotește, unghiul de rotație j se modifică în timp, adică este o funcție a timpului t:
Această ecuație se numește ecuaţie mișcarea de rotație a unui corp rigid.
Principalele caracteristici cinematice ale mișcării de rotație a unui corp rigid sunt viteza sa unghiulară w accelerația unghiulară e.
Dacă în timp D t= t1 + t corpul face o întoarcere cu Dj = j1 –j, atunci viteza unghiulară medie a corpului pentru această perioadă de timp va fi egală cu
(1.16)
Pentru a determina valoarea vitezei unghiulare a unui corp la un moment dat t găsiți limita raportului dintre creșterea unghiului de rotație Dj și intervalul de timp D t când acesta din urmă tinde spre zero:
(2.17)
Astfel, viteza unghiulară a corpului la un moment dat este numeric egală cu prima derivată a unghiului de rotație în timp. Semnul vitezei unghiulare w coincide cu semnul unghiului de rotație al corpului j: w > 0 pentru j > 0 și invers, dacă j < 0.apoi w < 0. Dimensiunea vitezei unghiulare este de obicei 1 / s, deoarece radianul este adimensional.
Viteza unghiulară poate fi reprezentată ca un vector w , a cărui valoare numerică este egală cu dj / dt, care este îndreptată de-a lungul axei de rotație a corpului în direcția din care se vede rotația mergând în sens invers acelor de ceasornic.
Modificarea vitezei unghiulare a unui corp în timp caracterizează accelerația unghiulară e. Prin analogie cu găsirea valorii medii a vitezei unghiulare, vom găsi o expresie pentru determinarea valorii accelerației medii:
(2.18)
Apoi, din expresie se va determina accelerația unui corp rigid la un moment dat de timp
(2.19)
adică accelerația unghiulară a corpului la un moment dat este egală cu prima derivată a vitezei unghiulare sau cu derivata a doua a unghiului de rotație al corpului în raport cu timpul. Dimensiunea accelerației unghiulare este 1/s 2.
Accelerația unghiulară a unui corp rigid, precum și viteza unghiulară, pot fi reprezentate ca un vector. Vectorul accelerației unghiulare coincide în direcție cu vectorul vitezei unghiulare în timpul mișcării accelerate a unui vârtej rigid și este îndreptat în direcția opusă în timpul mișcării decelerate.
După ce am stabilit caracteristicile mișcării unui corp rigid în ansamblu, trecem la studiul mișcării punctelor sale individuale. Luați în considerare un punct M un corp rigid situat la o distanţă h de axa de rotaţie r (fig. 2.3).
Când corpul se rotește, punctul M va descrie o circumferențială p. De raza h centrată pe axa de rotație și situată într-un plan perpendicular pe această axă. Dacă în timpul dt are loc o rotație elementară a corpului la un unghi dj , ideea Mîn același timp, efectuează o mișcare elementară de-a lungul traiectoriei sale dS = h * dj ,. Apoi viteza punctului M a fost determinată din expresie
(2.20)
Viteza se numește viteza liniară sau periferică a punctului M.
Astfel, viteza liniară a unui punct al unui corp rigid rotativ este numeric egală cu produsul vitezei unghiulare a corpului cu distanța de la acest punct la axa de rotație. Deoarece pentru toate punctele corpului viteza unghiulară w; are aceeași valoare, apoi din formula vitezei liniare rezultă că vitezele liniare ale punctelor corpului în rotație sunt proporționale cu distanța lor față de axa de rotație. Viteza liniară a unui punct al unui corp rigid este un vector n direcționat tangențial la cercul descris de punctul M.
Dacă distanța de la axa de rotație a unui cântec solid până la un anumit punct M considerat ca vectorul rază h al punctului M, atunci vectorul viteză liniară al punctului v poate fi reprezentat ca produsul vectorial al vectorului viteză unghiulară w vector rază h:
V = l * h (2/21)
Într-adevăr, rezultatul produsului vectorial (2.21) este un vector egal ca modul cu produsul w * h și direcționat (Fig. 2.5) perpendicular pe planul în care se află cei doi factori, în direcția din care cea mai apropiată coincidență a primul factor cu al doilea este observat mergând în sens invers acelor de ceasornic, adică de-a lungul tangentei la traiectoria punctului M.
Astfel, vectorul rezultat din produsul vectorial (2.21) corespunde ca mărime și direcție vectorului vitezei liniare a punctului M.
Orez. 2.5
Pentru a găsi o expresie pentru accelerație A punctul М, efectuăm diferențierea în timp a expresiei (2.21) pentru viteza punctului
(2.22)
Ținând cont de faptul că dj / dt = e, a dh / dt = v, scriem expresia (2.22) sub forma
unde a g și, respectiv, an, componentele tangente și normale ale accelerației totale a unui punct al corpului în timpul mișcării de rotație, determinate din expresiile
Componenta tangenţială a acceleraţiei totale a unui punct al corpului (acceleraţia tangenţială) la caracterizează modificarea vectorului viteză în valoare absolută şi este direcţionată tangenţial la traiectoria punctului corpului în direcţia vectorului viteză în timpul acceleraţiei. mișcare sau în sens opus în timpul mișcării decelerate. Mărimea vectorului de accelerație tangențială a unui punct al corpului în timpul mișcării de rotație a unui corp rigid este determinată de expresia
(2,25)
Accelerație completă componentă normală (accelerare normală) A" apare din cauza unei modificări a direcției vectorului viteză a unui punct la vopsirea unui solid. După cum reiese din expresia (2.24) pentru accelerația normală, această accelerație este îndreptată de-a lungul razei h spre centrul cercului de-a lungul căruia se mișcă punctul. Modulul vectorului normal de accelerație al unui punct în timpul mișcării de rotație a unui corp rigid este determinat luând în considerare (2.20) prin expresia
Rotirea unui corp rigid în jurul unei axe fixe (axa de rotație) mișcarea sa se numește astfel încât punctele corpului aflate pe axa de rotație rămân nemișcate pe toată durata mișcării.
Fie axa de rotație o axă care poate avea orice direcție în spațiu. O direcție a axei este considerată pozitivă (fig. 28).
Prin axa de rotație desenăm un plan fix și unul mobil, fixat pe un corp rotativ. Lăsați ambele planuri să coincidă în momentul inițial de timp. Apoi, în momentul de față, poziția planului mobil și a corpului rotativ însuși poate fi determinată de unghiul diedric dintre plane și unghiul liniar corespunzător dintre liniile drepte situate în aceste plane și perpendicular pe axa de rotație. Unghiul se numește unghiul de rotație al corpului.
Poziția corpului față de cadrul de referință selectat este complet determinată în orice moment dacă este dată ecuația
unde este oricare, funcție de două ori diferențiabilă a timpului. Această ecuație se numește ecuația de rotație a unui corp rigid în jurul unei axe fixe.
Un corp care se rotește în jurul unei axe fixe are un grad de libertate, deoarece poziția sa este determinată prin specificarea unui singur parametru - unghiul.
Unghiul este considerat pozitiv dacă este reprezentat în sens invers acelor de ceasornic și negativ - în direcția opusă, atunci când este privit din direcția pozitivă a axei. Traiectoriile punctelor unui corp atunci când acesta se rotește în jurul unei axe fixe sunt cercuri situate în planuri perpendiculare pe axa de rotație.
Pentru a caracteriza mișcarea de rotație a unui corp rigid în jurul unei axe fixe, introducem conceptele de viteză unghiulară și accelerație unghiulară. Viteza unghiulară algebrică a unui corpîn orice moment în timp, prima derivată temporală a unghiului de rotație în acest moment se numește, i.e. ... Este o valoare pozitivă când corpul se rotește în sens invers acelor de ceasornic, deoarece unghiul de rotație crește cu timpul, și negativă când corpul se rotește în sensul acelor de ceasornic, deoarece unghiul de rotație scade.
Modulul de viteză unghiulară este desemnat. Atunci
Accelerația unghiulară algebrică a unui corp prima derivată temporală a vitezei algebrice se numește, i.e. derivata a doua a unghiului de rotație. Prin urmare, notăm modulul de accelerație unghiulară
Dacă la, atunci viteza unghiulară algebrică crește cu timpul și, prin urmare, corpul se rotește cu o viteză accelerată în momentul în cauză în sens pozitiv (în sens invers acelor de ceasornic). La și, corpul se rotește cu accelerație în direcția negativă. Dacă este, atunci avem o rotație mai lentă în direcția pozitivă. La și, rotația încetinită este în direcția negativă.
Aceasta este o mișcare în care toate punctele corpului se mișcă în cercuri, ale căror centre se află pe axa de rotație.
Poziția corpului este dată de unghiul diedru (unghiul de rotație).
= (t) este ecuația mișcării.
Caracteristicile cinematice ale corpului:
- viteza unghiulara, s -1;
- accelerația unghiulară, s -2.
Mărimile și pot fi reprezentate ca vectori 
situat pe axa de rotație, direcția vectorului 
este de așa natură încât de la capătul său se vede rotația corpului mergând în sens invers acelor de ceasornic. Direcţie 
coincide cu 
, dacă 
> despre.
P 
poziţie punctele corpului: M 0 M 1 = S = h.
Viteză puncte 
; în care 
.
Unde 
;
;
.
Accelerare puncte ale corpului, 
- accelerația de rotație (în cinematică punctuală - tangentă - 
):
- accelerația șocului (în cinematică punctuală - normală - 
).
Module: 
;
;
.
Rotație uniformă și egală
1. Uniformă: = const, 
;
;
- ecuația mișcării.
2. Echivalent: = const, 
;
;
;
;
- ecuația mișcării.
2
). Acționarea mecanică este formată dintr-un scripete 1, o curea 2 și roți în trepte 3 și 4. Aflați viteza cremalierei 5, precum și accelerația punctului M la momentul t 1 = 1 s. Dacă viteza unghiulară a scripetelui este 1 = 0,2t, s -1; R1 = 15; R3 = 40; r3 = 5; R4 = 20; r 4 = 8 (în centimetri).
Viteza Reiki
;
;
;
.
Unde 
;
;
, s -1.
Din (1) și (2) obținem, vezi.
Accelerația punctului M.
, s -2 la t 1 = 1 s; a = 34,84 cm/s 2.
3.3 Mișcarea plan-paralelă (plană) a unui corp rigid
E 
acea mișcare în care toate punctele corpului se mișcă în planuri paralele cu un plan fix.
Toate punctele corpului de pe orice linie dreaptă perpendiculară pe planul fix se mișcă în același mod. Prin urmare, analiza mișcării plane a unui corp se reduce la studiul mișcării unei figuri plane (secțiunea S) în planul său (xy).
Această mișcare poate fi reprezentată ca un set de mișcări de translație împreună cu unele arbitrar punctul selectat a, numit stâlp, și mișcarea de rotație în jurul polului.
Ecuații de mișcare figură plată
x a = x a (t); y a = y a; j = j (t)
Caracteristici cinematice ki al unei figuri plate:
- viteza polilor si acceleratia; w, e - viteza unghiulara si acceleratia unghiulara (nu depind de alegerea polului).
Avea 
egalizarea mișcării oricărui punct figura plană (B) poate fi obținută prin proiectarea egalității vectoriale 
pe axele x și y
x 1 B, y 1 B - coordonatele punctului din sistemul de coordonate asociat formei.
Determinarea vitezelor punctuale
1). Mod analitic.
Cunoscând ecuațiile mișcării x n = x n (t); y n = y n (t), găsim 
;
;
.
2). Teorema distribuției vitezei.
D 
diferențierea egalității 
, primim 
,
- viteza punctului B când figura plană se rotește în jurul polului A; 
;
Formula de distribuție a vitezelor punctelor unei figuri plate 
.
CU 
viteza punctului M al unei roți care rulează fără alunecare
;
.
3). Teorema proiecției vitezei.
Proiecțiile vitezelor a două puncte ale corpului pe axa care trece prin aceste puncte sunt egale. Proiectarea egalității 
pe axa x avem
P 
exemplu
Determinați viteza de intrare a apei v N pe cârma navei, dacă este cunoscută 
(viteza centrului de greutate al navei), b și b K (unghiuri de deriva).
Soluție: .
4). Centru de viteză instantanee (IMC).
Vitezele punctelor în timpul mișcării plane a unui corp pot fi determinate prin formulele mișcării de rotație, folosind conceptul de MCS.
MCS - un punct asociat cu o figură plată, a cărei viteză la un moment dat este egală cu zero (v p = 0).
În cazul general, MCS este punctul de intersecție al perpendicularelor pe direcțiile vitezelor celor două puncte ale figurii.
Luând punctul P ca pol, avem un punct arbitrar
, atunci 
Unde 
- viteza unghiulară a figurii și 
,acestea. vitezele punctelor unei figuri plate sunt proporționale cu distanțele lor față de MCS.
|
Posibile cazuri de găsire a MDC |
|||
|
Rulare fără alunecare |
|||
|
|
|
|
|
|
|
MCS - la infinit | ||
Cazul b corespunde unei distribuții instantanee a vitezei de translație.
1
). Pentru o poziție dată a mecanismului, găsiți v B, v C, v D, w 1, w 2, w 3, dacă în momentul de față v A = 20 cm / s; BC = CD = 40 cm; OC = 25 cm; R = 20 cm.
Soluție MCS patinoar 1 - punctul P 1:
cu -1; 
cm/s.
Legătura MDS 2 - punctul P 2 de intersecție a perpendicularelor pe direcțiile vitezelor punctelor B și C:
cu -1; 
cm/s; 
cm/s; 
cu -1.
2). Sarcina Q este ridicată cu ajutorul unui tambur în trepte 1, a cărui viteză unghiulară este w 1 = 1 s -1; R1 = 3r1 = 15 cm; AE || BD. Aflați viteza v C a axei blocului mobil 2.
Aflați vitezele punctelor A și B:
v A = v E = w 1 * R 1 = 15 cm / s; v B = v D = w 1 * r 1 = 5 cm / s.
Blocul MCS 2 este punctul P. Atunci 
, Unde 
;
;
cm/s.
Orez. 6.4
O astfel de mișcare a corpului în care oricare dintre punctele sale (Ași Vîn fig. 6.4) rămân staționari, numită rotație în jurul unei axe staționare.
Se poate arăta că în acest caz orice punct al corpului care se află pe linia dreaptă care leagă punctele Aw B.
Axa care trece prin aceste puncte se numește axa de rotatie corp; direcția sa pozitivă este aleasă în mod arbitrar (Fig. 6.4).
Orice punct M corp, care nu se află pe axa de rotație, descrie un cerc, al cărui centru este situat pe axa de rotație (Fig. 6.4).
Poziția corpului cu o axă fixă de rotație z(Figura 6.5) poate fi descris folosind doar un parametru scalar - unghiul de rotație (pag... Acesta este unghiul dintre două plane trasate prin axa de rotație: un plan fix Nși mobil - R, legat rigid de corp (Fig. 6.5). Pentru pozitiv luăm direcția unghiului opus mișcării în sensul acelor de ceasornic, când este privit de la capătul axei z.(indicat printr-o săgeată arcuită în Fig.6.5). Unitatea de măsură pentru unghiul în sistemul SI este 1 radian „57,3 °. Dependența funcțională a unghiului de rotație în timp
determină complet mișcarea de rotație a corpului în jurul unei axe fixe. Prin urmare, egalitatea (6.3) se numește ecuația de rotație a unui corp rigid în jurul unei axe fixe.
Viteza de rotație a corpului este caracterizată de viteza unghiulară cu corp, care este definit ca derivata unghiului de rotație în raport cu timpul
și are dimensiunea rad / s (sau s "").
A doua caracteristică cinematică a mișcării de rotație este accelerația unghiulară - derivata vitezei unghiulare a corpului:
Dimensiunea accelerației unghiulare este rad / s 2 (sau Cu~ 2).
Cometariu. Simboluri cu si? v ale acestei prelegeri sunt desemnate algebric valorile vitezei unghiulare și ale accelerației unghiulare. Semnele lor indică direcția de rotație și natura acesteia (accelerată sau încetinită). De exemplu, dacă cu = f> 0, apoi unghiul (R crește cu timpul și, prin urmare, corpul se rotește în direcția de referință (R.
Viteza și accelerația fiecărui punct al unui corp în rotație nu este dificil de raportat la viteza unghiulară și accelerația unghiulară a acestuia. Luați în considerare mișcarea unui punct arbitrar M corp (Figura 6.6).
Deoarece traiectoria sa este un cerc, coordonata arcului.9 puncte M după întoarcerea corpului într-un unghi voi
Unde h- distanta fata de punct M faţă de axa de rotaţie (Fig. 6.6).
Diferențiând ambele părți ale acestei egalități în funcție de timp, obținem, ținând cont de (5.14) și (6.4):
unde r r este proiecția vitezei punctului pe tangenta r, îndreptată către punctul de referință al arcului v și unghiul
Mărimea accelerației normale a punctului M conform (5.20) și (6.6) va fi
și proiecția accelerației sale tangențiale pe tangenta r conform (5.19) și (6.5)
Modul de accelerare punct complet M
Direcțiile vectorilor v, a, a „, a, pentru cazul când f> 0 și f> 0 sunt prezentate în fig. 6.7.
Exemplu 1. Mecanismul de transmisie este format din roți / și 2, care sunt conectate într-un punct LA astfel încât atunci când se rotesc, alunecarea reciprocă este absentă. Ecuația de rotație a roții 1:
direcția de citire a unghiului pozitiv (R indicată printr-o săgeată arc în fig. 6.8.
Dimensiunile mecanismului sunt cunoscute: G= 4 cm, R2 = 6 cm, r 2 = 2 cm.
Aflați viteza și accelerația unui punct M roțile 2 pentru momentul de timp / | = 2 s.
Soluţie. Când mecanismul roții se mișcă 1 și 2 se rotesc în jurul axelor fixe care trec prin puncte 0 și 0 2 perpendicular pe planul din fig. 6.8. Aflați viteza unghiulară și accelerația unghiulară a roții eu la momentul t = 2 s, folosind definițiile de mai sus (6.4) și (6.5) ale acestor mărimi:
Semnele lor negative indică faptul că în momentul de față t - Roata de 2 s / se rotește în sensul acelor de ceasornic (opus direcției de citire a unghiului (R) și această rotație este accelerată. Datorită absenței alunecării reciproce a roților euși 2 vectori ai vitezelor punctelor lor în punctul de contact LA trebuie să fie egal. Să exprimăm modulul acestei viteze în termeni de viteze unghiulare ale roților, folosind (6.6):
Din ultima egalitate, exprimăm modulul vitezei unghiulare a roții 2 și găsim valoarea acestuia pentru momentul specificat de timp 6 = 2 s:
Direcția vitezei La(fig. 6.9) indică faptul că roata 2 se rotește în sens invers acelor de ceasornic și, prin urmare, Oh> 0. Din (6.10) și din ultima inegalitate se vede că vitezele unghiulare ale roților diferă printr-un factor negativ constant (- r1g 2): cu 2 = r (/ g 2). Dar apoi derivatele acestor viteze - accelerațiile unghiulare ale roților trebuie să difere prin același factor: e 2 =? ] (-g] / g 1) = - 2-(-4/2) = 4s ~ 2.
Găsim valorile vitezei și accelerației punctului M roata în trepte 2 folosind formulele (6.6) - (6.9):
Direcțiile vectorilor v și, a și d / sunt prezentate în Fig. 6.9.
