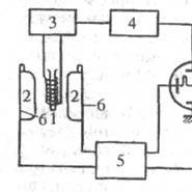
Stikls- šis materiāls ir īpašs un atšķiras no citiem būvmateriāliem.
Šis būvmateriāls ir ārkārtīgi trausls un lielākoties ir caurspīdīgs.
Tāpēc, pirms pērkat stiklu un strādājat ar to, jums jāsāk iepirkšanās ar instrumentu.
Taču nevajadzētu pirkt pirmo instrumentu, ar kuru saskaraties, jo tas var būt nekvalitatīvs un nespēs sagriezt stiklu pēc vajadzības.
Ir ļoti svarīgi noteikt, kāds instruments jums ir nepieciešams, jo ir vairāki stikla griezēju veidi:
- Veltnis;
- Dimants;
- Eļļains;
Veltnis
Rullīšu stikla griezējam stikla griešanai ir iebūvēts speciāls veltnis, kas izgatavots no ļoti izturīga volframa-kobalta sakausējuma. Parastais veltņa diametrs ir 6,6 mm, šis veltņa diametrs ļauj griezt stiklu līdz 4 mm biezumā.
Dimants
Dimanta stikla griezējs ir aprīkots ar attiecīgi mazu dimantu, šis dimants griež stiklu. Dimanta cietība ir labi zināma, tāpēc to jau sen izmanto stikla griešanai.
Mūsdienās, tāpat kā iepriekš, dimanta stikla griezējs tiek uzskatīts par labāko instrumentu stikla griešanai.
Eļļains
Pirms neilga laika stikla griezēju sarakstam tika pievienots eļļas stikla griezējs.
Tas būtībā ir uzlabots rullīšu rīks, kura rokturī ir iebūvēts rezervuārs, lai veltni piegādātu smērvielu. Šī smērviela saista daļiņas, kas radušās griežot stiklu, vienlaikus nodrošinot vienmērīgu kustību. Šis stikla griezējs var griezt stiklu līdz 20 mm.
- Pirms iegādāties jebkura veida stikla griezējus, vislabāk ir lūgt pārdevējam pārbaudīt.
- Ja esat apmierināts ar instrumentu, tad varat to iegādāties, bet iegādājieties to, kas jums tika demonstrēts.
Kā griezt stiklu
Stikla loksni nav tik viegli sagriezt, kā šķiet sākumā. Lai veiktu stikla griezumu, ir nepieciešama sagatavošana.
Sagatavošana
- Pilnīgi jauns stikls būs tikai rūpīgi jānotīra no putekļiem un jānoslauka ar avīzi, audums šādam darbam nav piemērots.
- Ja jāgriež vecs stikls, vispirms to vajadzētu attaukot, pēc tam stiklu labi nomazgāt ar ūdeni un mazgāšanas līdzekļiem.
- Pēc visām iepriekšminētajām manipulācijām stikls būs jāizžāvē slēgtā un tīrā telpā.
Izgriezt stiklu
Sagatavošanas darbi ietver arī stikla griešanu un konteineru sagatavošanu atkritumu savākšanai. Jābūt diviem konteineriem, tas ir, sīko atkritumu savākšanai un lielāku savākšanai, kas nākotnē var kaut kam noderēt.
Griežot stiklu, vislabāk ir sākt ar vienkāršu logu stiklu un pēc tam pāriet uz sarežģītākām iespējām.
Stikla griešanas tehnika

Lietojot dimanta stikla griezēju, jums tas jātur pašā roktura apakšā un jāvelk gluda līnija gar lineālu, gandrīz nespiežot uz stikla.
Griežot stiklu ar rullīšu stikla griezēju Nepieciešams neliels spiediens un, stikla griezējam kustoties, uz stikla virsmas parādās bālgana svītra, dziļāka nekā izmantojot dimanta instrumentu.
Iespējamās kļūdas
Kad ir stikla upe, ir divas kļūdas:
- Spiediens ar stikla griezēju var būt pārāk spēcīgs;
- Stikla griezējs tiek veikts vairākas reizes vienā un tajā pašā vietā.
Griežot stiklu, mēģiniet vienmērīgi nospiest instrumentu visā griezuma garumā.
Ja, griežot stiklu, pamanāt šķembas, tas nozīmē tikai to, ka pārāk spēcīgi piespiežat instrumentu. Lai no tā izvairītos, samaziniet spiedienu uz stikla griezēju.
Nekad nevelciet dubultā pa griezuma līniju, jo tas var sabojāt instrumentu.
Pēdējais posms ir stikla laušana
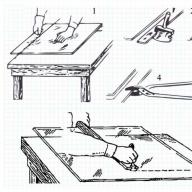
Plāns stikls tiek izsists ar rokām. Jau nogrieztais stikla gabals jānovieto uz galda malas tā, lai griešanas līnija būtu augšpusē un nedaudz izvirzītos ārpus galda malas, un stikla galvenajai daļai jāatrodas uz galda.
Ar vienu roku jāpiespiež stikla loksne, ar otru jāsatver stikla izvirzītā daļa un ar roku uzmanīgi jāpiespiež stikls.
Ja nolaužamā maliņa ir maza un to nevar nolauzt ar roku, izmantojiet knaibles.
Zināšanas par tērauda griešanas teoriju ļauj šīs zināšanas pielietot praksē. Tas ir, jūs varat paņemt nelielu stikla gabalu un praktizēt uz tā.
Pēc tam, kad praktiski izmēģināsit stikla griešanu, turpmāk būsiet pārliecinātāks par savām prasmēm. Mēs ceram, ka šī informācija ir noderīga. Vēlam veiksmi un pacietību!
Izvēles nodarbību cikls par tēmu “Griešanas problēmu risināšana”
Paskaidrojuma piezīme
Pamata mērķi ko mēs ievietojam izvēles nodarbībās, ir šādas:
paralēla pārsūtīšana,
pagriezties,
centrālā simetrija un dažādas šo pārvērtību kompozīcijas.
Prezentēt materiālu par daudzstūru griešanas veidiem;
Veicināt skolēnos prasmju veidošanos, lai garīgi veiktu tādas pārvērtības kā:
UN visu nodarbību galvenais mērķis: panākt pozitīvas izmaiņas telpiskās domāšanas spējās.
Izvēles nodarbībās piedāvātie uzdevumi ir radoši pēc būtības, to risināšanai studentiem nepieciešams: prasmes:
spēja veikt garīgās transformācijas, kas maina skolēnu prātā esošo attēlu atrašanās vietu, struktūru, struktūru;
spēja mainīt attēlu gan atrašanās vietā, gan struktūrā vienlaicīgi un atkārtoti veikt atsevišķu darbību kompozīcijas.
Tematiskais plānojums:
1. Anketa Nr.1 – 1 stunda.
2. Griešanas problēmas. R tipa griešana – 1 stunda.
3. P tipa griešana – 1 stunda.
4. Q tipa griešana – 1 stunda.
5. S tipa griešana – 1 stunda.
6. T veida griešana – 1 stunda.
7. Anketa Nr.2 – 1 stunda.
Veidojot izvēles nodarbību ciklu, izmantoti žurnālu “Kvant”, “Matemātika skolā” uzdevumi un G.Lindgrēna grāmata.
Vadlīnijas: Iepazīstinot skolēnus ar problēmām, iesakām šīs problēmas izskatīt precīzi atbilstoši G. Lindgrēnas piedāvātajiem griešanas veidiem, kas ļauj, no vienas puses, šīs problēmas klasificēt, no otras puses, klasē risināt problēmas, kas saistītas ar telpisku. dažādu sarežģītības līmeņu transformācijas (otrais un trešais tips, kas darbojas ar attēliem, saskaņā ar I. S. Jakimanskaju). Darbā ar 7.-9.klašu skolēniem iesakām izmantot izvēles nodarbību uzdevumus.
Nodarbība Nr.1
Tēma: Problēmu griešana. R tipa griešana (racionāla griešana).
Mērķis: Iepazīstināt studentus ar griešanas problēmas jēdzienu, izskaidrot griešanas veida R būtību, analizējot uzdevumu risinājumu šāda veida griešanai, problēmu risināšanas procesā, veicināt prasmju veidošanos garīgi veikt darbības (griešana, pievienošana, pārgriešana, virpošana, paralēla pārvietošana), tādējādi veicinot telpiskās domāšanas attīstību.
Aprīkojums: papīrs, krāsainas pastas, šķēres, plakāts.
Metode: skaidrojoši - ilustratīvi.
Skolotājs: plakāts uz tāfeles:
Shēma: problēmu griešana
Griešanas problēmas
1) Izgrieziet figūru vairākās figūrās
3) Pārveidojiet vienu vai vairākas formas citā formā
2) No dotajām figūrām saloki figūriņu
Starp visām griešanas problēmām lielākā daļa ir racionālas griešanas problēmas. Tas ir saistīts ar faktu, ka šādus griezumus ir viegli izdomāt un uz tiem balstītās mīklas nav pārāk vienkāršas un nav pārāk sarežģītas.
Problēmas R - griešanai
1) Izgrieziet figūru vairākās (galvenokārt vienādās) figūrās
3) Pārveidojiet vienu vai vairākas formas noteiktā formā
2) Pievienojiet figūru no dotajām (galvenokārt vienādām) figūrām
3.1. Izmantojot pakāpienu griešanu
3.2. Neizmantojot pakāpienu griešanu
Iepazīsimies ar uzdevumu risinājumu katram griešanas veidam R.
II posms: problēmu risināšanas posms
Metodes: daļēja meklēšana
Uzdevums Nr.1(AII) : Izgrieziet kvadrātu ar četru kvadrātu malu divās vienādās daļās. Atrodiet pēc iespējas vairāk griešanas veidu.
Piezīme: Jūs varat griezt tikai gar šūnu malām.
Risinājums:






Šādus griezumus skolēni meklē savās kladēs, tad skolotājs apkopo visas skolēnu atrastās griešanas metodes.
Problēma Nr.2(AII) : Sagrieziet šīs formas divās vienādās daļās.
Piezīme: Jūs varat griezt ne tikai gar šūnu malām, bet arī pa diagonāli.




Šādus griezumus skolēni ar skolotāja palīdzību meklē savās kladēs.
Laukumam ir daudz brīnišķīgu īpašumu. Taisni leņķi, vienādas malas, simetrija piešķir tai vienkāršību un formas pilnību. Uz salokāmiem kvadrātiem no vienādas un dažādas formas daļām ir daudz mīklu.
UZ  piemērs uzdevums Nr.3(BII) :
Jums tiek dotas četras identiskas daļas. Garīgi izveidojiet no tiem kvadrātu, katru reizi izmantojot visas četras daļas. Veiciet visus testus uz papīra. Prezentējiet sava risinājuma rezultātus ar roku zīmēta zīmējuma veidā.
piemērs uzdevums Nr.3(BII) :
Jums tiek dotas četras identiskas daļas. Garīgi izveidojiet no tiem kvadrātu, katru reizi izmantojot visas četras daļas. Veiciet visus testus uz papīra. Prezentējiet sava risinājuma rezultātus ar roku zīmēta zīmējuma veidā.
Risinājums:

Daļās sagriezts šaha galdiņš, kas pareizi jāsaloka, ir viena no populārākajām un zināmajām mīklām. Montāžas sarežģītība ir atkarīga no tā, cik daļās plāksne ir sadalīta.
Es piedāvāju šādu uzdevumu:
Problēma Nr.4(BII) : Saliec šaha galdiņu no attēlā redzamajām daļām.



Risinājums:

Problēma #5(VII) : Sagrieziet “Laivu” divās daļās, lai tās varētu salocīt kvadrātā.

Risinājums:

1) sagriež divās daļās kā attēlā
apgrieziet vienu no daļām (t.i., pagrieziet)
Problēma Nr.6(VII): Jebkuru no trim figūrām var sagriezt divās daļās, no kurām viegli salocīt kvadrātu. Atrodiet šādus griezumus.
A)  b)
b) 
V) 
Risinājums:
1. daļas paralēla pārnešana attiecībā pret 2. daļu
1. daļas rotācija attiecībā pret 2. daļu
)  b)
b)  V)
V) 
Problēma Nr.7(VII): Taisnstūris ar malām 4 un 9 vienības ir sagriezts divās vienādās daļās, kuras, pareizi salokot, varētu iegūt kā kvadrātu.

griezums tiek veikts pakāpienu veidā, kuru augstums un platums ir vienādi;
figūra tiek sadalīta daļās un viena daļa tiek pārvietota par vienu (vai vairākiem) pakāpieniem uz augšu, novietojot to uz citas daļas.
Risinājums:

1. daļas paralēla pārnešana

Problēma Nr.9(VII): Sagriežot attēlā redzamo figūru divās daļās, salokiet tās kvadrātā tā, lai krāsainie kvadrāti būtu simetriski attiecībā pret visām kvadrāta simetrijas asīm.

Risinājums:

1. daļas paralēla pārnešana
Problēma Nr.9(ВIII): Kā jāizgriež divi kvadrāti 3 x 3 un 4 x 4, lai iegūtās daļas varētu salocīt vienā kvadrātā? Izdomājiet vairākus veidus. Centieties iztikt ar pēc iespējas mazāk detaļu.
Risinājums:
paralēla detaļu pārvietošana
Veids: 
Veids: 

paralēlā tulkošana un rotācija
veids:
4 ceļi: 
paralēla detaļu pārvietošana un rotācija
Skolēni ar skolotāja palīdzību meklē griezumus.
Problēma Nr.10(AIII): attēlā redzamā figūra jāsadala 6 vienādās daļās, veicot griezumus tikai pa režģa līnijām. Cik daudzos veidos jūs varat to izdarīt?

Risinājums: Divi iespējamie risinājumi.


Problēma Nr.11(BII): no dotajām figūrām izveido šaha dēli.

![]()


Risinājums:

Problēma Nr.12(BIII): pārveidojiet 3 x 5 taisnstūri par 5 x 3 taisnstūri, nepagriežot atbilstošās daļas.
Piezīme: izmantojiet pakāpienu griešanu.
Risinājums:(paralēlā pārsūtīšana)


Problēma Nr.13(BIII): sagrieziet formu 2 daļās ar vienu griezumu, lai izveidotu 8 x 8 kvadrātu.

Risinājums:


2. daļas rotācija attiecībā pret 1. daļu
Vadlīnijas: R tipa griešanas problēmas ir dažas no vienkāršākajām un interesantākajām. Daudzas šāda veida griešanas problēmas ietver vairākas risināšanas metodes, un studentu patstāvīgais šo problēmu risinājums var palīdzēt noteikt visas risināšanas metodes. 1., 2., 3., 6., 7., 8., 10., 12., 13. uzdevumā skolēni iesaistās darbā ar figūru tēlu, veicot garīgās transformācijas (“griešana”, pievienošana, rotācija, paralēla pārnešana). 4., 5., 9., 11. uzdevums ietver studentu darbu ar modeļiem (no papīra), tieši griežot figūru ar šķērēm un veicot matemātiskas transformācijas (rotācija, paralēlā tulkošana), lai rastu problēmu risinājumus. 1., 2., 3., 4., 5., 6., 7., 8., 11., 13. uzdevumi - otrajam darbības veidam ar attēliem, 9., 10., 12. uzdevumi - trešajam darbības veidam ar attēliem.
Nodarbība Nr.2
Tēma: griešanas veids P (P paralelograma nobīde).
Mērķis: Izskaidrojiet P tipa griešanas būtību, analizējot šāda veida griešanas problēmu risināšanu, vienlaikus veicinot prasmju veidošanos garīgi veikt darbības (griešana, pievienošana, pārgriešana, paralēla pārvietošana), tādējādi veicinot telpiskās domāšanas attīstība.
Aprīkojums:
I posms: Orientēta stadija
Metode: problemātiska prezentācija.
Skolotājs izvirza problēmu (risiniet uzdevumu Nr. 1) un parāda tās risinājumu.
Uzdevums Nr.1(BIII): pārveidojiet paralelogramu ar malām 3 un 5 cm par jaunu paralelogramu ar tādiem pašiem leņķiem kā sākotnējam paralelogramam, kura viena no malām ir 4 cm.
Risinājums: 1)


4)

ABC D – paralelograms
AB = 3, A D=5
veikt griezumu AO VO = D K = 4;
pārvietot 1. daļu uz augšu (paralēlā translācija) pa labi pa griezuma līniju, līdz punkts O nokrīt uz malas DC turpinājumu;
veikt griezumu KA', lai KA' || DC ;
un Δ AA'K ievietojam padziļinājumā, kas atrodas zem punkta O (Δ AA'K paralēla pārnešana pa taisnu līniju AO).
KVO D ir vēlamais paralelograms (КD = 4)
KDO= A.D.C. SLIKTI = 1 + 4,
1 = 2 un 4 = 3 – guļus šķērsām uz paralēlām līnijām.
Tāpēc BAD = 2 + 3 = BOC = BKD, BAD = BKD utt.
U
Problēmas ar P maiņu
Pārveidojiet vienu vai vairākas formas citā formā
lasītājs:P veida griešanas būtība:
mēs izgatavojam šī attēla sadaļu, kas atbilst uzdevuma prasībām;
veicam grieztās daļas paralēlu pārvietošanu pa griezuma līniju, līdz grieztās daļas augšdaļa sakrīt ar oriģinālās figūras (paralelogrammas) otras puses turpinājumu;
veicam otru griezumu paralēli paralelograma malai, iegūstam vēl vienu daļu;
Mēs veicam tikko grieztās daļas paralēlu pārvietošanu pa pirmā griezuma līniju, līdz virsotnes sakrīt (detaļu ievietojam padziļinājumā).
II posms: problēmu risināšanas posms
Metodes: skaidrojoši - ilustratīvi
Problēma Nr.2(BII): pārveidojiet 5 x 5 kvadrātu par taisnstūri, kura platums ir 3.
Risinājums:
1)
 2) – 3)
2) – 3)
 4)
4)

sadaļa AO / VO = D T = 3
paralēla pārnese ΔABO pa taisnu līniju AO līdz punktam O (DC)
griezt TA’ / TA’ || CD
Δ AA 'T ar paralēlu pārvietošanu pa taisni AO.
TBOD ir vēlamais taisnstūris (TB = 3).
Problēma Nr.3(VIII): salokiet trīs vienādus kvadrātus vienā lielā kvadrātā.
Piezīme: salokiet trīs kvadrātus taisnstūrī, pēc tam izmantojiet P nobīdi.
Risinājums:
S pr = 1,5 * 4,5 = 6,75


1)
 2) – 3)
2) – 3)

4)

Problēma Nr.4(BIII): izgrieziet 5 x 1 taisnstūri kvadrātā

Piezīme: izdariet iegriezumu AB (A W = ), izmantojiet P nobīdi taisnstūrim XYWA.
), izmantojiet P nobīdi taisnstūrim XYWA.

Risinājums:
1)

2) – 3)
 4)
4)
 5)
5)


Problēma Nr.5(ВIII): pārveidojiet krievu Н kvadrātā.
Piezīme: veiciet griezumu, kā parādīts attēlā, salokiet iegūtās daļas taisnstūrī.

Risinājums:



Problēma Nr.6(BIII): pārveidojiet trīsstūri par trapecveida formu.
Piezīme: veiciet griezumu, kā parādīts attēlā.

Risinājums:



pagriezt 1. daļu;
AB sadaļa;
ΔАВС paralēla pārnešana pa AB līdz punktam B (FM)
griezt VAI / VAI || FM;
ΔAOR ar paralēlu transportu pa AB. Punkts P sakrīt ar punktu B;
OFBC ir vēlamā trapece.
Problēma Nr.7(ВIII): izveidojiet vienu kvadrātu no trim vienādiem grieķu krustiem.
Risinājums:






Problēma Nr.8(BIII): pārveidojiet burtu T kvadrātā.
Piezīme: Vispirms no burta t izgrieziet taisnstūri.
Risinājums:
S t = 6 (2. vienība), Skv = (  )
2
)
2
 pagrieziens
pagrieziens 

paralēlo defisu sastāvs

MV = KS = 
Problēma Nr.9(ВIII): pārzīmējiet attēlā redzamo karogu kvadrātā.
Piezīme. Vispirms pārveidojiet karogu par taisnstūri
Risinājums:
 pagrieziens
pagrieziens 
S fl = 6,75 AB = C D = Skv = (
Skv = (  )
2
)
2

paralēla pārsūtīšana

Vadlīnijas: Iepazīstinot skolēnus ar P tipa griešanas problēmām, iesakām, risinot konkrētu uzdevumu, iepazīstināt ar šī griešanas veida būtību. Mēs iesakām problēmas vispirms risināt uz modeļiem (no papīra), tieši griežot figūras ar šķērēm un veicot paralēlu pārsūtīšanu, un pēc tam uzdevumu risināšanas procesā no figūru modeļiem pārejot uz darbu ar ģeometrisku formu attēliem, veicot garīgās transformācijas (griešana, paralēla pārvietošana).
Nodarbība Nr.3
Tēma: Griešanas veids Q (Q ir četrstūra nobīde).
Mērķis: Ieskicēsim Q griešanas veida būtību, risinot problēmas šāda veida griešanai, vienlaikus veicinot prasmju veidošanos garīgi veikt darbības (griešana, pievienošana, centrālā simetrija, rotācija, paralēla pārvietošana), tādējādi veicinot telpiskās domāšanas attīstība.
Aprīkojums: papīrs, krāsainas pastas, šķēres.
I posms: Orientēta stadija
Metode: problemātiska prezentācija.
Skolotājs izvirza skolēniem problēmu (atrisiniet uzdevumu Nr. 1) un parāda risinājumu.
Uzdevums Nr.1(BIII): pārveidojiet šo četrstūri par jaunu četrstūri.

Risinājums:


mēs veicam HP griezumu tā, lai VN = MN, PF = DF;
veikt griezumu ME / ME || Saule;
veikt griezumu RT / RT || AD ;
Δ 3 un Δ 1 tiek pagriezti pulksteņrādītāja virzienā attiecībā pret 2. daļu;
1. daļa ar paralēlu pārnesi pa taisni HF līdz punktam T AR;
AMCP ir nepieciešamais četrstūris (ar malām CP un AM (var norādīt nosacījumā)).
Problēma Nr.2(BIII): pārveidojiet četrstūri par jaunu četrstūri (garu četrstūri).

Risinājums:


(pagriezt 1. daļu attiecībā pret punktu O, līdz OU sakrīt ar AO);
(pagriezt daļu (1 – 2) attiecībā pret punktu T, līdz VT sakrīt ar WT);
XAZW ir nepieciešamais četrstūris.
Problēmās, izmantojot Q griezumus, tiek veikti griezumi, un izgrieztie gabali tiek pakļauti rotācijas transformācijai.
Uzdevumi priekš Q griešana
pārveidot doto formu (četrstūri) citā formā (četrstūrī)
Daudzās problēmās tiek izmantoti Q nobīdes elementi, lai trijstūri pārveidotu par kādu četrstūri vai otrādi (trijstūris kā "četrstūris", kura vienai no malām ir nulle garums).
II posms: problēmu risināšanas posms
Problēma Nr.3(VII): no trijstūra tiek izgriezts neliels trīsstūris, kā parādīts attēlā. Pārkārtojiet mazo trīsstūri, lai izveidotu paralelogramu.


Pagrieziet 1. daļu attiecībā pret punktu P, līdz KR sakrīt ar MR.
AOO'M ir nepieciešamais paralelograms.
Problēma Nr.4(BII, BIII): Kuru no šiem trijstūriem var pārvērst par taisnstūriem, veicot vienu (divus) griezumus un pārkārtojot iegūtās daļas?
1)
 2)
2)
 3)
3)
 4)
4)

5)

Risinājums:
1)


5)


1), 5) viens griezums (griezums – trijstūra viduslīnija)
2)


3)


4)


2), 3), 4) divi griezumi (1. griezums – viduslīnija, 2. griezums – augstums no trijstūra virsotnes).
Problēma Nr.5(VII): izveidojiet trapecveida formu trīsstūrī.

Risinājums:



sadaļa KS (AK = KB)
rotācija ΔKVS ap punktu K tā, lai segmenti KV un KA būtu izlīdzināti.
Δ FCD vēlamo trīsstūri.
Problēma Nr.6(ВIII): Kā sadalīt trapeci formās, no kurām var izveidot taisnstūri?

Risinājums:


1) VAI sadaļa (AO = OB, OR┴AD)
2) griezt TF (CT = TD, TF ┴AD)
1. daļas rotācija attiecībā pret punktu O tā, lai AO un BO būtu izlīdzināti.
Pagrieziet 2. daļu attiecībā pret punktu T, lai DT un CT būtu saskaņoti.
PLMF – taisnstūris.
III posms: mājasdarbu iestatīšana.
Problēma Nr.7(VIII) : pārvērst jebkuru trīsstūri par taisnleņķa trīsstūri.
komentēt:
1) vispirms pārveidojiet patvaļīgu trīsstūri par taisnstūri.
2) taisnstūris taisnstūrī.
Risinājums:
 pagrieziens
pagrieziens 

Problēma Nr.8(VII): pārveidojiet patvaļīgu paralelogramu par trīsstūri, veicot tikai vienu griezumu.
Risinājums:
 pagrieziens
pagrieziens

Pagriezt 2. daļu ap punktu O par 180º (simetrijas centrs)
Vadlīnijas: Mēs iesakām Q griešanas būtības kopsavilkumu
veikt konkrētu problēmu risināšanas procesā. Galvenās matemātiskās transformācijas, ko izmanto, risinot problēmas šāda veida griešanai, ir: rotācija (jo īpaši centrālā simetrija, paralēlā tulkošana). 1., 2., 7. uzdevums – praktiskām darbībām ar ģeometrisku formu modeļiem, 3., 4., 5., 6., 8. uzdevums ietver darbu ar ģeometrisku formu attēliem. 3., 4., 5., 8. uzdevums – otrajam darbības veidam ar attēliem, 1., 2., 4., 6., 7. uzdevums – trešajam darbības veidam ar attēliem.
Nodarbība Nr.4.
Tēma: S tipa griešana.
Mērķis: Izskaidrojiet S tipa griešanas būtību, risinot problēmas šim griešanas veidam, vienlaikus veicinot prasmju veidošanos garīgi veikt darbības (griešana, pievienošana, pārklāšanās, pagriešana, paralēla pārvietošana, centrālā simetrija), tādējādi veicinot telpiskās domāšanas attīstība.
Aprīkojums: papīrs, krāsainas pastas, šķēres, kodu pozitīvi.
es posms: Orientēta stadija.
Metode: skaidrojošs un ilustratīvs.
Uzdevums Nr.1(VII): kā paralelogramu, kura malas ir 3,5 cm un 5 cm, sagriezt paralelogramā ar malām 3,5 cm un 5,5 cm, izdarot tikai vienu “griezumu”?

Risinājums:


1) uzzīmējiet segmentu (nogrieztu) CO = 5,5 cm, sadaliet paralelogramu divās daļās.
2) paralelograma AK pretējai pusei pieliekam trijstūri COM. (t.i. paralēla ∆ COM pārnešana uz segmentu SA SA virzienā).
3) CAOO` ir vēlamais paralelograms (CO = 5,5 cm, CA = 3,5 cm).
Uzdevums Nr.1(ВIII): parādiet, kā kvadrātu var sagriezt 3 daļās, lai no tām izveidotu taisnstūri, kura viena mala ir divreiz lielāka par otru.
Risinājums:


Izveidojiet kvadrātu ABCD
zīmēsim diagonāli AC
Uzzīmēsim pusi no diagonālā BD segmenta OD (OD ┴AC), OD = ½ AC. No iegūtajām 3 daļām izveidojiet taisnstūri (garums AC, platums AD
Priekš šī:
veikt paralēlu 1. un 2. daļas pārvietošanu. 1. daļa (∆1) virzienā D A, ∆2 virzienā AB uz segmentu AB.
AOO`C ir vēlamais taisnstūris (ar malām AC, OA = ½ AC).
Skolotājs: Mēs esam apskatījuši 2 problēmu risinājumu, šo problēmu risināšanā izmantoto griešanas veidu tēlaini sauc par S-griešanu.
S - griešana būtībā ir viena paralelograma pārveidošana citā paralelogramā.
Šī griezuma būtība sekojošajā:
mēs veicam griezumu, kas vienāds ar vajadzīgā paralelograma malu;
veicam nogrieztās daļas paralēlu pārvietošanu, līdz sakrīt paralelograma vienādās pretējās malas (t.i., nogriezto daļu uzklājam uz paralelograma pretējo pusi)
Atkarībā no uzdevuma prasībām, griezumu skaits būs atkarīgs.
Apskatīsim šādus uzdevumus:
Uzdevums Nr.3(BII): sadaliet paralelogramu divās daļās, no kurām varat pievienot taisnstūri.
Uzzīmēsim patvaļīgu paralelogramu.
Risinājums:


no punkta B pazeminiet VN augstumu (VN┴AD)
Veiksim paralēlu ∆ AVN pārnešanu uz segmentu BC virzienā uz BC.
Uzzīmējiet iegūtā taisnstūra zīmējumu.
VNRS – taisnstūris.
Uzdevums Nr.4(BIII): paralelograma malas ir 3 un 4 cm. Pārvērtiet to paralelogramu ar 3,5 cm malām, veicot divus griezumus.
Risinājums:

1)


2)


Vēlamais paralelograms.
Kopumā S-griešana balstās uz sloksņu uzklāšanas metodi, kas ļauj atrisināt jebkuru daudzstūru pārveidošanas problēmu.
Iepriekšminētajās problēmās to viegluma dēļ mēs atteicāmies no svītru uzlikšanas metodes, lai gan visus šos risinājumus var iegūt, izmantojot šo metodi. Bet sarežģītākos uzdevumos nevar iztikt bez svītrām.
Īsumā svītru metode izpaužas šādi:
1) Izgrieziet (ja nepieciešams) katru daudzstūri (pārveidojamo daudzstūri un daudzstūri, kurā jāpārveido sākotnējais daudzstūris) daļās, no kurām var salocīt divas sloksnes.
2) Novietojiet sloksnes vienu virs otras piemērotā leņķī, vienas no tām malām vienmēr novietojot vienādi attiecībā pret otras sloksnes elementiem.
3) Šajā gadījumā visas līnijas, kas atrodas 2 sloksņu kopējā daļā, parādīs nepieciešamo griezumu vietas.
Vēstule S, ko lieto terminā "S-cut", nāk no angļu valodas Strip - strip.
II posms: problēmu risināšanas posms
Izmantojot 3. uzdevumu kā piemēru, pārbaudīsim, vai svītru uzlikšanas metode dod vēlamo risinājumu.
Problēma Nr.3(VII): sadaliet paralelogramu divās daļās, no kurām varat pievienot taisnstūri.
Risinājums:
1)

2)

3) 
1) no paralelograma iegūstam sloksni
2) taisnstūru svītras
3) uzlieciet 2. sloksni uz 1. sloksnes, kā parādīts 3. attēlā
4) iegūstam nepieciešamo uzdevumu.
Problēma Nr.5(BIII): vienādsānu trīsstūrī ir atzīmēti sānu malu viduspunkti un to projekcijas uz pamatni. Caur atzīmētajiem punktiem tiek novilktas divas taisnas līnijas. Parādiet, ka iegūtos gabalus var izmantot, lai izveidotu rombu.
Risinājums:


2., 3. daļa – rotācija ap punktu
4. daļa - paralēla pārnešana
Šajā uzdevumā jau ir norādīta trīsstūru izgriešana; mēs varam pārbaudīt, vai tas ir S-izgriezums.

Problēma Nr.6(BIII): pārveidojiet trīs grieķu krustus kvadrātā (izmantojot svītras).
Risinājums:



1) 



Uz krustiņu sloksnes uzliekam rūtiņu sloksni tā, lai punkts A un punkts C piederētu krustiņu joslas malām.
∆АВН = ∆СD B, tāpēc kvadrāts sastāv no ∆АВС un ∆АВМ.
III posms: mājasdarbu iestatīšana
Problēma Nr.7(BIII): pārveidojiet šo taisnstūri citā taisnstūrī, kura malas atšķiras no sākotnējā taisnstūra malām.
Piezīme. Apskatiet 4. problēmas risinājumu.
Risinājums:


sadaļa AO (AO – vajadzīgā taisnstūra platums);
griezt DP / DP AO (DP – vajadzīgā taisnstūra garums);
paralēla ∆AVO pārnešana gaisa kuģa virzienā uz gaisa kuģa segmentu;
paralēla ∆АPD pārnešana uz segmentu AO AO virzienā;
Nepieciešams PFED taisnstūris.
Problēma Nr.8(BIII): regulāru trīsstūri sadala daļās ar segmentu; no šīm daļām izveidojiet kvadrātu.
Piezīme. Pārklājot sloksnes, varat pārbaudīt, vai šis ir S izgriezums.



2. daļas rotācija ap punktu O;
3. daļas rotācija ap punktu C;
4. daļas paralēla pārnešana
Papildu uzdevums Nr.9(BII): Izgrieziet paralelogramu pa taisnu līniju, kas iet caur tā centru, lai iegūtos divus gabalus varētu salocīt rombā.
Risinājums:


O QT
QT griezums;
1. daļa, paralēli pārnesot uz BC segmentu virzienā BC (CD un AB ir apvienoti).
Vadlīnijas: S – griešana – viens no grūtākajiem griešanas veidiem. Mēs iesakām šīs griešanas būtību ieskicēt konkrētos uzdevumos. S - griešanas problēmu risināšanas nodarbībās mēs iesakām izmantot problēmas, kurās ir norādītas griešanas figūras, un no iegūtajām daļām ir jāpievieno vajadzīgā figūra, tas izskaidrojams ar studentu grūtībām patstāvīgi īstenot sloksņu uzlikšanas metodi, kas ir S būtība - griešana. Tajā pašā laikā skolēniem pieejamākos uzdevumos (piemēram, 3., 5., 8. uzdevumā) skolotājs var parādīt, kā strēmelīšu uzlikšanas metode ļauj iegūt uzdevuma nosacījumos dotos griezumus. 4., 5., 6., 8., 9. uzdevums – praktiskām darbībām ar ģeometrisko formu modeļiem, 1., 2., 3., 7. uzdevums – darbam ar ģeometrisku formu attēliem. 1., 3., 9. uzdevums – otrajam darbības veidam ar attēliem, 2., 4., 5., 6., 7., 8. uzdevums – trešajam darbības veidam ar attēliem.
Nodarbība Nr.5
Tēma: T veida griešana.
Mērķis: Izskaidrojiet S tipa griešanas būtību, analizējot šāda veida griešanas problēmu risināšanu, vienlaikus veicinot prasmju veidošanos garīgi veikt darbības (griešana, pievienošana, virpošana, paralēla pārvietošana), tādējādi veicinot griešanas veidu attīstību. telpiskā domāšana.
Aprīkojums: papīrs, krāsainas pastas, šķēres, krāsainas pastas, kodu pozitīvi.
I posms: Orientēta stadija
Metode: skaidrojošs un ilustratīvs
Skolotājs: Izmantojot T veida izgriezumu problēmu risināšanai, ir jāizveido mozaīka un turpmākais pārklājums. S-veida griešanai izmantotās sloksnes var iegūt no mozaīkām. Tāpēc flīzēšanas metode vispārina sloksnes metodi.
Apskatīsim T veida griešanas būtību, izmantojot problēmu risināšanas piemēru.
Uzdevums Nr.1(BIII): pārveidojiet grieķu krustu kvadrātā.
1) pirmais solis ir pārveidot sākotnējo daudzstūri par mozaīkas elementu (un tas ir nepieciešams);
2) no šiem elementiem veidojam mozaīku Nr.1 (mozaīku veidojam no grieķu krustiem);
5) visas līnijas, kas atrodas abu mozaīku kopējā daļā, parādīs nepieciešamo griezumu vietas.


II posms: problēmu risināšanas posms
Metode: daļēji - meklēt
Problēma Nr.2(BIII): Grieķu krustu sagriež trīs daļās, salieciet šīs daļas taisnstūrī.
Piezīme: mēs varam pārbaudīt, vai šis griezums ir T veida griezums.
Risinājums:


1. daļas rotācija ap punktu O;
pagrieziet 2. daļu ap punktu A.

Problēma Nr.3(BIII): Izgrieziet izliekto četrstūri pa divām taisnēm, kas savieno pretējo malu viduspunktus. Parādiet, ka no iegūtajiem četriem gabaliem vienmēr ir iespējams pievienot paralelogramu.


2. daļas rotācija ap punktu O (vai simetrijas centru) par 180;
3. daļas rotācija ap punktu C (vai simetrijas centru) par 180;
1. daļa – paralēla pārnešana.
Parādīsim mozaīku, no kuras iegūts šis griezums.

Problēma Nr.4(BIII): trīs identiski trīsstūri tika izgriezti pa dažādām mediānām. Salieciet sešus iegūtos gabalus vienā trīsstūrī.



Risinājums:
1) no šiem trijstūriem veidojam trijstūrus kā 1. attēlā (centrālā simetrija);
2) veidojam vēl vienu trīsstūri no trim jauniem trijstūriem (vienādas malas sakrīt).

Parādīsim, kā šīs sadaļas tika veidotas, izmantojot mozaīkas.

Problēma Nr.5(BIII): Grieķu krusts tika sagriezts gabalos, un no šiem gabaliem tika izveidots taisnleņķa vienādsānu trīsstūris.
Risinājums:



1. daļa centrālā simetrija;
3. daļa centrālā simetrija;
3. un 4. daļa – pagrieziens.

Problēma Nr.6(BIII): izgrieziet šo figūru kvadrātā.

Risinājums:

1. daļas rotācija ap punktu O;
3. daļa pagrieziet 90 ap punktu A.

Problēma Nr.7(BIII): Grieķu krustu sagriež paralelogrammā (ir doti griezumi).
Risinājums:


2. daļa – paralēla pārnešana attiecībā pret 1. daļu;
3. daļa paralēla pārvietošana pa griezuma līniju.
III posms: mājasdarbu iestatīšana.
Problēma Nr.8(BIII): divi identiski papīra izliekti četrstūri ar griezumiem: pirmais pa vienu no diagonālēm un otrais pa otru diagonāli. Pierādīt, ka iegūtās daļas var izmantot paralelograma veidošanai.


Risinājums: pagriezienu sastāvs.

Problēma Nr.9(BIII): izveidojiet kvadrātu no diviem identiskiem grieķu krustiem.


Risinājums:


Vadlīnijas: T - griešana - vissarežģītākais griešanas veids, kas veido S tipa griezumus. Mēs iesakām problēmu risināšanas procesā izskaidrot T veida griešanas būtību. Sakarā ar mozaīkas metodes ieviešanas sarežģītību skolēniem, kas ir T veida griešanas būtība, klasē iesakām izmantot uzdevumus, kuros ir norādīta griešana un ir nepieciešams iegūt vēlamo figūru no iegūtajām figūras daļām, izmantojot matemātiskās transformācijas (rotācija, paralēlā tulkošana). Tajā pašā laikā skolēniem pieejamākos uzdevumos skolotājs var parādīt, kā iegūt griešanas datus, izmantojot mozaīkas metodi. 5. nodarbībā piedāvātie uzdevumi ir paredzēti trešajam darbības veidam ar attēliem un iesaista skolēnus darbā ar ģeometrisko figūru modeļiem, veicot rotāciju un paralēlo tulkošanu.
Skolotāja ievadvārdi:
Nedaudz vēsturiskā fona: daudzi zinātnieki ir interesējušies par problēmu risināšanu kopš seniem laikiem. Daudzu vienkāršu griešanas problēmu risinājumus atrada senie grieķi un ķīnieši, bet pirmo sistemātisko traktātu par šo tēmu uzrakstīja Abul-Vef. 20. gadsimta sākumā ģeometri sāka nopietni risināt problēmas, kas saistītas ar figūru sagriešanu mazākās daļās un pēc tam citas figūras konstruēšanu. Viens no šīs sadaļas dibinātājiem bija slavenais mīklu dibinātājs Henrijs E. Dudenijs.
Mūsdienās mīklu mīļotāji aizraujas ar griešanas problēmu risināšanu, jo nav universālas metodes šādu problēmu risināšanai, un ikviens, kurš uzņemas tās risināt, var pilnībā demonstrēt savu atjautību, intuīciju un radošās domāšanas spēju. (Nodarbības laikā norādīsim tikai vienu no iespējamiem griešanas piemēriem. Var pieņemt, ka skolēni var nonākt pie kādas citas pareizas kombinācijas - no tā nav jābaidās).
Šī nodarbība ir paredzēta praktiskas nodarbības veidā. Sadaliet apļa dalībniekus grupās pa 2-3 cilvēkiem. Katrai grupai sniedziet skolotāja iepriekš sagatavotas figūras. Skolēniem ir lineāls (ar dalījumiem), zīmulis un šķēres. Ar šķērēm ir atļauts veikt tikai taisnus griezumus. Sagriežot figūru gabalos, no tām pašām daļām jāizgatavo vēl viena figūra.
Griešanas uzdevumi:
1). Mēģiniet sagriezt attēlā redzamo figūru 3 vienādas formas daļās:
Padoms: mazās formas izskatās pēc burta T.


2). Tagad sagrieziet šo figūru 4 vienādas formas daļās:
Padoms: Ir viegli uzminēt, ka mazas figūriņas sastāvēs no 3 šūnām, taču nav daudz figūru ar trim šūnām. Ir tikai divi veidi: stūris un taisnstūris.
3). Sadaliet figūru divās vienādās daļās un izmantojiet iegūtās daļas, lai izveidotu šaha dēli.


Padoms: Iesakiet sākt uzdevumu no otrās daļas, it kā iegūstot šaha galdiņu. Atcerieties, kāda forma ir šaha galdiņam (kvadrāts). Saskaitiet pieejamo šūnu skaitu garumā un platumā. (Atcerieties, ka jābūt 8 šūnām).


4). Mēģiniet sagriezt sieru astoņos vienādos gabalos ar trim naža kustībām.


Padoms: mēģiniet sagriezt sieru gareniski.


Uzdevumi patstāvīgam risinājumam:
1). Izgrieziet papīra kvadrātu un rīkojieties šādi:
· sagriež 4 daļās, no kurām var izveidot divus vienādus mazākus kvadrātus.
· sagriež piecās daļās - četros vienādsānu trīsstūros un vienā kvadrātā - un salokiet tās tā, lai iegūtu trīs kvadrātus.
Sargsjans Romāns
Pētniecisko darbu “Griešanas problēmas” pabeidza 8. klases skolēni
Skolēni tiek iepazīstināti un izzināti ar figūru griešanas paņēmieniem spēlēs “Pentamino”, “Tangrammas”, mīklās, teorēmu pierādīšanā.
Lejupielādēt:
Priekšskatījums:
Lai izmantotu prezentāciju priekšskatījumus, izveidojiet Google kontu un piesakieties tajā: https://accounts.google.com
Slaidu paraksti:
Priekšskatījums:
Pētnieciskais darbs par tēmu
"Problēmu samazināšana"
Izpilda: Romāns Sargsjans, Anastasija Šavrova,
8. klases skolēni
MBOU "Severomuyskaya vidusskola"
Vadītājs: matemātikas skolotāja Ogarkova I.I.
- Ievads
- Vēsturiska atsauce
- Spēle "Pentamino"
- Spēle "Tangram"
- Problēma "Kūka"
- Uzdevums Nr. 4 - “Izgriezt taisnstūri”
- Uzdevums Nr. 5 - “Izgriezt divus kvadrātus”
- Uzdevums Nr. 6 - “Izgriezt divus kvadrātus-2”
- Problēma #7 — krusts
- Uzdevums Nr.8 – Krusts -2
- Uzdevums Nr.9 - Kvadrāts 8*8
- Uzdevums Nr. 10 Paralelograma laukums
- Uzdevums Nr. 11 Trapeces laukums
- Uzdevums Nr. 12 Trijstūra laukums
- Secinājums
- Literatūra.
Ievads
“Problēmu risināšana ir līdzīga praktiska māksla
peldēt, slēpot vai spēlēt klavieres;
to var iemācīties tikai atdarinot labo
paraugi un pastāvīgi praktizē"
D. Poija
Aizraušanās ar matemātiku bieži sākas, domājot par problēmu, kas jums īpaši patīk. Bagāts šādu problēmu avots ir dažādas olimpiādes – skolas, pilsētas, tālmācības, starptautiskās. Gatavojoties olimpiādēm, apskatījām daudz un dažādus uzdevumus un noskaidrojām problēmu grupu, kuru risināšanas pieeja mums šķita interesanta un oriģināla. Tie ir griešanas uzdevumi. Mums radās jautājumi: kāda ir šādu problēmu īpatnība, vai ir īpašas metodes un paņēmieni griešanas problēmu risināšanai.
Atbilstība (2. slaids)
- Matemātiķi atklāj jaunas sakarības starp matemātiskiem objektiem. Šī darba rezultātā tiek atrastas vispārīgas metodes dažādu problēmu risināšanai. Un šīs problēmas saņem standarta risināšanas metodes, pārejot no radošās kategorijas uz tehnisko kategoriju, tas ir, pieprasot to risināšanai izmantot jau zināmas metodes.
- Griešanas uzdevumi palīdz skolēniem pēc iespējas agrāk veidot ģeometriskus jēdzienus, izmantojot dažādus materiālus. Risinot šādas problēmas, rodas skaistuma, likuma un kārtības sajūta dabā.
Pētījuma objekts: griešanas uzdevumi
Studiju priekšmets: dažādas griešanas problēmas, metodes un paņēmieni to risināšanai.
Pētījuma metodes: modelēšana, salīdzināšana, vispārināšana, analoģijas, literāro un interneta resursu izpēte, informācijas analīze un klasifikācija.
(3. slaids) Galvenāpētījuma mērķisir paplašināt zināšanas par griešanas uzdevumu dažādību.
Lai sasniegtu šo mērķi, mēs paredzam atrisināt sekojošo uzdevumi: (4. slaids)
- izvēlieties nepieciešamo literatūru
- iemācīties sagriezt ģeometriskās figūras daļās, kas nepieciešamas vienas vai otras ģeometriskas formas sastādīšanai, izmantojot to īpašības un īpašības;
- iemācīties pierādīt, ka figūru laukumi ir vienādi, sagriežot tās atsevišķās daļās un pierādot, ka šīs figūras ir vienādi saliktas;
- veikt ģeometriskos pētījumus un projektēšanu dažādu veidu problēmu risināšanā.
- atlasīt materiālu pētniecībai, izvēlēties galveno, interesantu, saprotamu informāciju
- analizēt un sistematizēt saņemto informāciju
- atrast dažādas metodes un paņēmienus griešanas problēmu risināšanai
- klasificē pētāmās problēmas
- atrast veidus, kā pārveidot: trīsstūri par viendaļīgu paralelogramu; paralelograms vienādmalu trijstūrī; trapecveida vienādmalu trīsstūrī.
- Izveidojiet sava darba elektronisku prezentāciju
Hipotēze: Iespējams, ka griešanas problēmu daudzveidība, to “izklaidējošais” raksturs un vispārīgu noteikumu un metožu trūkums to risināšanai rada grūtības skolēniem to izskatīšanā. Pieņemsim, ka, rūpīgāk izpētot griešanas uzdevumus, mēs pārliecināsimies par to aktualitāti, oriģinalitāti un lietderību.
Risinot griešanas uzdevumus, mums nav vajadzīgas zināšanas par planimetrijas pamatiem, bet mums būs nepieciešama atjautība, ģeometriskā iztēle un diezgan vienkārša ģeometriskā informācija, kas ir zināma ikvienam.
(5. slaids) Vēsturiskais fons
Griešanas problēmas kā puzles veids ir piesaistījušas uzmanību kopš seniem laikiem. Pirmo traktātu, kurā aplūkotas griešanas problēmas, uzrakstīja slavenais arābu astronoms un matemātiķis no Horasanas Abu al-Vefa (940.–998. g.). 20. gadsimta sākumā, pateicoties periodikas straujajai izaugsmei, uzmanību kā plašu sabiedrības slāņu izklaidēšanas līdzekli piesaistīja figūru sagriešanas noteiktās daļās un pēc tam komponēšanas jaunā figūrā problēmu risināšana. Tagad ģeometri šīs problēmas ir uztvēruši nopietni, jo īpaši tāpēc, ka to pamatā ir senā problēma par vienāda izmēra un vienādi saliktām figūrām, kas aizsākās senajos ģeometros. Pazīstami speciālisti šajā ģeometrijas nozarē bija slavenie izklaidējošās ģeometrijas klasiķi un mīklu veidotāji Henrijs E. Dudenijs un Harijs Lindgrēns.
Enciklopēdija dažādu griešanas uzdevumu risināšanai ir Harija Lindgrēna grāmata “Griešanas ģeometrija”. Šajā grāmatā jūs varat atrast ierakstus daudzstūru sagriešanai noteiktās formās
Apsverot risinājumus griešanas problēmām, jūs saprotat, ka nav universāla algoritma vai metodes. Dažreiz iesācējs ģeometrs savā risinājumā var ievērojami pārspēt pieredzējušāku cilvēku. Šī vienkāršība un pieejamība ir pamatā tādu spēļu popularitātei, kuru pamatā ir, piemēram, šādu problēmu risināšana- (6. slaids) pentominoTetris, tangrama "radinieki".
(7. slaids) Spēle “Pentamino” Spēles noteikumi
Spēles būtība ir dažādu objektu siluetu konstruēšana plaknē. Spēle ietver dažādu gabalu pievienošanu no noteiktā pentomino komplekta. Pentomino komplektā ir 12 figūriņas, no kurām katra ir veidota no pieciem vienādiem kvadrātiem, un kvadrāti atrodas viens otram blakus tikai aiz sāniem.
Spēle "Tangram" (8. slaids)
Spēlē "tangram" no septiņiem pamatelementiem var izveidot ievērojamu skaitu figūru.Visām saliktajām figūrām jābūt ar vienādu laukumu, jo samontēti no identiskiem elementiem. No tā izriet, ka:
- Katrā saliktajā figūrā noteikti jāietver visi septiņi elementi.
- Veidojot figūru, elementi nedrīkst pārklāties viens ar otru, t.i. atrodas tikai vienā plaknē.
- Figūru elementiem jāatrodas blakus viens otram.
Uzdevumi
Tangrama spēlē ir 3 galvenās uzdevumu kategorijas:
- Viena vai vairāku veidu atrašana noteiktas figūras konstruēšanai vai elegants pierādījums figūras konstruēšanas neiespējamībai.
- Meklējot veidu, kā ar vislielāko izteiksmīgumu vai humoru (vai abus kopā) attēlot dzīvnieku, cilvēku un citu atpazīstamu priekšmetu siluetus.
- Dažādu kombinatoriskās ģeometrijas problēmu risināšana, kas rodas saistībā ar figūru kompozīciju no 7 tanām.
3. uzdevums (9. slaids)
Kūka , dekorēts ar rozēm, tika sadalīts gabalos ar trim taisniem griezumiem, lai katrā gabalā būtu tieši viena roze. Kāds ir lielākais rožu skaits, kas varētu būt uz kūkas?
Komentārs. Problēmas risinājums ir balstīts uz aksiomas pielietojumu:"Taisna līnija sadala plakni divās pusplaknēs."Jāattēlo visi iespējamie trīs taisnu līniju izvietojuma gadījumi. No attēla kļūst skaidrs, ka vislielākais detaļu skaits - 7 - tiek iegūts, kad līnijas krustojas pa pāriem. Tāpēc uz kūkas varēja būt ne vairāk kā 7 rozes.
4. uzdevums (10. slaids)
Izgrieziet taisnstūri, ax2a tādās daļās, ka no tām varēja izveidot vienādu izmēru tai:
1) taisnleņķa trīsstūris;
2) kvadrāts.
Problēmas risinājums ir skaidrs 2. un 3. attēlā.
5. uzdevums (11. slaids)
Izgrieziet divus kvadrātus1x1 un 3x3 tādās daļās, lai no tām varētu izveidot vienāda izmēra kvadrātu.
Komentārs. Šis uzdevums ir pārveidot figūru, kas sastāv no diviem kvadrātiem, vienāda izmēra kvadrātā. Jaunā laukuma platība ir 3 2 +1 2 , kas nozīmē, ka kvadrāta mala, kas ir vienāda ar šo kvadrātu summu, ir vienāda, t.i., ir taisnstūra hipotenūza ar kājiņām 3 un 1. Šāda kvadrāta konstrukcija ir skaidra no 4. attēla
6. uzdevums (12. slaids)
Izgrieziet divus nejaušus kvadrātustādās daļās, lai no tām varētu izveidot vienāda izmēra kvadrātu.
Problēmas risinājums ir skaidrs 5. attēlā. Jaunā kvadrāta laukums ir a 2 + b 2 , kas nozīmē, ka kvadrāta mala, kas vienāda ar šo kvadrātu summu, ir vienāda ar
i., tā ir taisnleņķa trijstūra hipotenūza ar kājiņām a un b.
7. uzdevums (13. slaids)
Krusts sastāv no pieciem kvadrātiem: viens kvadrāts atrodas centrā un pārējie četri blakus tā malām. Sagrieziet to gabalos, lai no tiem varētu izveidot vienāda izmēra kvadrātu.
Problēmas risinājums ir skaidrs 6. attēlā.
8. uzdevums (14. slaids)
Krusts sastāv no pieciem kvadrātiem: viens kvadrāts atrodas centrā un pārējie četri blakus tā malām. Kā nosegt lūka virsmu ar sešiem šādiem krustiem, kuru katra seja ir vienāda izmēra ar krustu.
Komentārs. Krusts ir uzlikts uz malas (7. att.), nav nepieciešams apgriezt un pārlīmēt “izvirzītās ausis” - tās pārvietojas uz blakus malu un nonāk pareizajās vietās. Aptinot “izvirzītās ausis” uz blakus esošajām virsmām, jūs varat pārklāt kuba virsmu ar sešiem krustiem (8. att.).
9. uzdevums (15. slaids)
Kvadrāts 8x8 sagriež četrās daļās, kā parādīts 9. attēlā. No iegūtajām daļām izveido 13x5 taisnstūri. Taisnstūra laukums ir 65, bet kvadrāta laukums ir 64. Paskaidrojiet, kur ir kļūda.
Punkts ir abstrakts objekts, kam nav mērīšanas īpašību: nav augstuma, nav garuma, nav rādiusa. Uzdevuma ietvaros svarīga ir tikai tā atrašanās vieta
Punktu norāda ar ciparu vai lielo (lielo) latīņu burtu. Vairāki punkti – ar dažādiem cipariem vai dažādiem burtiem, lai tos varētu atšķirt
punkts A, punkts B, punkts C
A B C1. punkts, 2. punkts, 3. punkts
1 2 3Jūs varat uz papīra uzzīmēt trīs punktus “A” un aicināt bērnu novilkt līniju caur diviem punktiem “A”. Bet kā saprast caur kurām? A A A
Līnija ir punktu kopa. Tiek mērīts tikai garums. Tam nav platuma vai biezuma
Apzīmēts ar mazajiem (mazajiem) latīņu burtiem
līnija a, līnija b, līnija c
a b cLīnija var būt
- slēgts, ja tā sākums un beigas atrodas vienā punktā,
- atvērt, ja tā sākums un beigas nav savienoti
slēgtas līnijas
atvērtās līnijas
Jūs izgājāt no dzīvokļa, veikalā nopirkāt maizi un atgriezāties dzīvoklī. Kādu līniju tu dabūji? Pareizi, slēgts. Jūs esat atgriezies savā sākuma punktā. Jūs izgājāt no dzīvokļa, veikalā nopirkāt maizi, iegājāt ieejā un sākāt runāt ar savu kaimiņu. Kādu līniju tu dabūji? Atvērt. Jūs neesat atgriezies savā sākuma punktā. Jūs izgājāt no dzīvokļa un veikalā nopirkāt maizi. Kādu līniju tu dabūji? Atvērt. Jūs neesat atgriezies savā sākuma punktā.- paši krustojas
- bez sevis krustojumiem
paškrustojošas līnijas
līnijas bez paškrustojumiem
- taisni
- salauzts
- greizs
taisnas līnijas
lauztas līnijas
izliektas līnijas
Taisne ir līnija, kas nav izliekta, tai nav ne sākuma, ne beigu, to var turpināt bezgalīgi abos virzienos
Pat tad, ja ir redzams neliels taisnes posms, tiek pieņemts, ka tā turpinās bezgalīgi abos virzienos
Apzīmēts ar mazo (mazo) latīņu burtu. Vai divi lielie (lielie) latīņu burti - punkti, kas atrodas uz taisnas līnijas
taisna līnija a
ataisne AB
BATiešs var būt
- krustojas, ja tiem ir kopīgs punkts. Divas līnijas var krustoties tikai vienā punktā.
- perpendikulāri, ja tie krustojas taisnā leņķī (90°).
- Paralēli, ja tie nekrustojas, tiem nav kopīga punkta.
paralēlas līnijas
krustojošās līnijas
perpendikulāras līnijas
Stars ir taisnas līnijas daļa, kurai ir sākums, bet nav beigu; to var turpināt bezgalīgi tikai vienā virzienā
Attēlā redzamā gaismas stara sākumpunkts ir saule.
Sv
Punkts sadala taisni divās daļās - divos staros A A
Staru apzīmē ar mazo (mazo) latīņu burtu. Vai divi lielie (lielie) latīņu burti, kur pirmais ir punkts, no kura sākas stars, bet otrais ir punkts, kas atrodas uz stara
stars a
asija AB
BAStari sakrīt, ja
- atrodas tajā pašā taisnē
- sākt vienā punktā
- vērsta vienā virzienā
stari AB un AC sakrīt
stari CB un CA sakrīt
C B ANogrieznis ir līnijas daļa, kuru ierobežo divi punkti, tas ir, tai ir gan sākums, gan beigas, kas nozīmē, ka tā garumu var izmērīt. Segmenta garums ir attālums starp tā sākuma un beigu punktu
Caur vienu punktu jūs varat novilkt jebkuru līniju skaitu, ieskaitot taisnas līnijas
Caur diviem punktiem - neierobežots skaits līkumu, bet tikai viena taisne
izliektas līnijas, kas iet caur diviem punktiem
BAtaisne AB
BANo taisnes tika “nogriezts” gabals un palika segments. Iepriekš redzamajā piemērā var redzēt, ka tā garums ir mazākais attālums starp diviem punktiem. ✂ B A ✂
Segmentu apzīmē ar diviem lielajiem (lielajiem) latīņu burtiem, kur pirmais ir punkts, kurā segments sākas, bet otrais ir punkts, kurā segments beidzas.
segments AB
BAProblēma: kur ir līnija, stars, segments, līkne?
Pārrauta līnija ir līnija, kas sastāv no secīgi savienotiem segmentiem, kas nav 180° leņķī
Garš segments tika “sadalīts” vairākos īsos
Pārtrauktās līnijas posmi (līdzīgi ķēdes posmiem) ir segmenti, kas veido lauzto līniju. Blakus esošās saites ir saites, kurās vienas saites beigas ir citas saites sākums. Blakus esošās saites nedrīkst atrasties uz vienas taisnas līnijas.
Pārrautas līnijas virsotnes (līdzīgi kalnu virsotnēm) ir punkts, no kura sākas lauztā līnija, punkti, kuros ir savienoti segmenti, kas veido lauzto līniju, un punkts, kurā lauztā līnija beidzas.
Lauzīta līnija tiek apzīmēta, uzskaitot visas tās virsotnes.
lauzta līnija ABCDE
polilīnijas A virsotne, polilīnijas B virsotne, polilīnijas C virsotne, polilīnijas D virsotne, polilīnijas E virsotne
bojāta saite AB, bojāta saite BC, bojāta saite CD, bojāta saite DE
saite AB un saite BC atrodas blakus
saite BC un saites CD atrodas blakus
saites CD un saite DE atrodas blakus
A B C D E 64 62 127 52Pārrautas līnijas garums ir tās saišu garumu summa: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Uzdevums: kura pārtrauktā līnija ir garāka, A kam ir vairāk virsotņu? Pirmajā rindā ir visas vienāda garuma saites, proti, 13 cm. Otrajā rindā ir visas vienāda garuma saites, proti, 49 cm. Trešajā rindā ir visas vienāda garuma saites, proti, 41 cm.
Daudzstūris ir slēgta polilīnija
Daudzstūra malas (izteicieni palīdzēs atcerēties: “iet visos četros virzienos”, “skrien uz māju”, “kurā galda pusē sēdēsi?”) ir lauztas līnijas saites. Daudzstūra blakus esošās malas ir lauztas līnijas blakus esošās saites.
Daudzstūra virsotnes ir lauztas līnijas virsotnes. Blakus esošās virsotnes ir daudzstūra vienas malas galapunkti.
Daudzstūris tiek apzīmēts, uzskaitot visas tā virsotnes.
slēgta polilīnija bez paškrustošanās, ABCDEF
daudzstūris ABCDEF
daudzstūra virsotne A, daudzstūra virsotne B, daudzstūra virsotne C, daudzstūra virsotne D, daudzstūra virsotne E, daudzstūra virsotne F
virsotne A un virsotne B atrodas blakus
virsotne B un virsotne C atrodas blakus
virsotne C un virsotne D atrodas blakus
virsotne D un virsotne E atrodas blakus
virsotne E un virsotne F atrodas blakus
virsotne F un virsotne A atrodas blakus
daudzstūra mala AB, daudzstūra mala BC, daudzstūra mala CD, daudzstūra mala DE, daudzstūra mala EF
puse AB un mala BC atrodas blakus
sānu BC un sānu CD atrodas blakus
Blakus atrodas CD puse un DE puse
mala DE un mala EF atrodas blakus
sānu EF un sānu FA atrodas blakus
A B C D E F 120 60 58 122 98 141Daudzstūra perimetrs ir lauztās līnijas garums: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Daudzstūri ar trim virsotnēm sauc par trīsstūri, ar četrām - par četrstūri, ar piecām - par piecstūri utt.